题目内容
已知函数f（x）=x3-3x+3，x∈[-2，2]，求此函数f（x）的最值．
考点：利用导数求闭区间上函数的最值
专题：导数的综合应用
分析：由已知得f'（x）=3x2-3，令f'（x）=0得：x=±1，由此列表讨论能求出函数f（x）的最值．
解答：
解：∵f（x）=x3-3x+3
∴f'（x）=3x2-3
令f'（x）=0得：x=±1
当x变化时，f'（x），f（x）的变化情况如下表：
…（6分）
∴当x=-1时，f（x）极大值=f（-1）=5；
当x=1时，f（x）极小值=f（-1）=1
又∵f（-2）=1，f（2）=5
∴f（x）max=5，f（x）min=1…（10分）
∴f'（x）=3x2-3
令f'（x）=0得：x=±1
当x变化时，f'（x），f（x）的变化情况如下表：
| x | （-2，-1） | -1 | （-1，1） | 1 | （1，2） |
| f'（x） | + | 0 | - | 0 | + |
| f（x） | ↗ | 极大值 | ↘ | 极小值 | ↗ |
∴当x=-1时，f（x）极大值=f（-1）=5；
当x=1时，f（x）极小值=f（-1）=1
又∵f（-2）=1，f（2）=5
∴f（x）max=5，f（x）min=1…（10分）
点评：本题考查函数在闭区间上的最大值和最小值的求法，是中档题，解题时要认真审题，注意导数性质的合理运用．
练习册系列答案
口算题天天练系列答案
相关题目
函数f（x）=1+
（-2≤x≤2）与函数g（x）=m（x-2）+4．若函数h（x）=f（x）-g（x）有两个零点时，参数m的取值范围为（ ）
| 4-x2 |
A、[
| ||||
B、（-
| ||||
C、[
| ||||
D、（
|
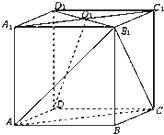已知正方体ABCD-A1B1C1D1中，面A1B1C1D1中心为O1．