题目内容
已知函数f(x)=a-
.
(1)若f(x)是奇函数,求a的值;
(2)证明函数f(x)在R上是增函数.
| 2 |
| 2x+1 |
(1)若f(x)是奇函数,求a的值;
(2)证明函数f(x)在R上是增函数.
考点:函数奇偶性的性质,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)根据奇函数定义求解.
(2)利用函数的单调性定义判断
(2)利用函数的单调性定义判断
解答:
解(1):函数f(x)=a-
,
∵f(x)是奇函数,∴f(-x)=-f(x),
即a-
=-(a-
),
化简得:a-2=-a,即可得a=1
(2):函数f(x)=1-
设x1<x2,可得2x1-2 x2<0,2 x1+1>0,2 x2+1>0,
作差 f(x1)-f(x2)=
<0
即f(x1)<f(x2),所以函数f(x)在R上是增函数
| 2x-1 |
| 2x+1 |
| 2 |
| 2x+1 |
∵f(x)是奇函数,∴f(-x)=-f(x),
即a-
| 2 |
| 2-x+1 |
| 2 |
| 2x+1 |
化简得:a-2=-a,即可得a=1
(2):函数f(x)=1-
| 2 |
| 2x+1 |
设x1<x2,可得2x1-2 x2<0,2 x1+1>0,2 x2+1>0,
作差 f(x1)-f(x2)=
| 2x1-2x2 |
| (2x1+1)(2x2+1) |
即f(x1)<f(x2),所以函数f(x)在R上是增函数
点评:本题考查了奇函数的定义,用函数单调性定义证明问题.

练习册系列答案
相关题目
数列{an}中,若a1=1,an+1=an+4,则下列各数中是{an}中某一项的是( )
| A、2007 | B、2008 |
| C、2009 | D、2010 |
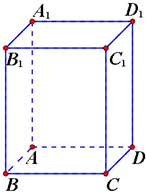 长方体ABCD-A1B1C1D1中,宽、长、高分别为3、4、5,现有一个小虫从A出发沿长方体表面爬行到C1来获取食物,求其路程的最小值.
长方体ABCD-A1B1C1D1中,宽、长、高分别为3、4、5,现有一个小虫从A出发沿长方体表面爬行到C1来获取食物,求其路程的最小值.
