题目内容
设等差数列{an}的前n项和为Sn,已知a3=24,a6=18.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}的前n项和Sn;
(Ⅲ)当n为何值时,Sn最大,并求Sn的最大值.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}的前n项和Sn;
(Ⅲ)当n为何值时,Sn最大,并求Sn的最大值.
考点:数列的求和,等差数列的通项公式,等差数列的前n项和
专题:等差数列与等比数列
分析:(Ⅰ)设等差数列{an}的公差是d,有等差数列的通项公式和题意求出d,再求出an;
(Ⅱ)先(Ⅰ)求出a1,代入sn=
化简即可;
(Ⅲ)根据Sn和n的取值范围,利用二次函数的性质,求出Sn的最大值及n的值.
(Ⅱ)先(Ⅰ)求出a1,代入sn=
| n(a1+an) |
| 2 |
(Ⅲ)根据Sn和n的取值范围,利用二次函数的性质,求出Sn的最大值及n的值.
解答:
解:(Ⅰ)设等差数列{an}的公差是d,
因为a3=24,a6=18,所以d=
=-2,
所以an=a3+(n-3)d=30-2n…(6分)
(Ⅱ)由(Ⅰ)得,a1=28,
所以sn=
=
=-n2+29n…(9分)
(Ⅲ)因为sn=-n2+29n,所以对称轴是n=
,
则n=14或15时,sn最大,
所以sn的最大值为s14=-(14)2+29×14=210…(12分)
因为a3=24,a6=18,所以d=
| a6-a3 |
| 6-3 |
所以an=a3+(n-3)d=30-2n…(6分)
(Ⅱ)由(Ⅰ)得,a1=28,
所以sn=
| n(a1+an) |
| 2 |
| n(28+30-2n) |
| 2 |
(Ⅲ)因为sn=-n2+29n,所以对称轴是n=
| 29 |
| 2 |
则n=14或15时,sn最大,
所以sn的最大值为s14=-(14)2+29×14=210…(12分)
点评:本题考查等差数列的通项公式、前n项和公式,以及利用二次函数的性质求出前n项和Sn的最值问题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
已知复数z满足(1+i)
=1-i(i是虚数单位),则复数z的虚部为( )
. |
| z |
| A、1 | B、-i | C、i | D、-1 |
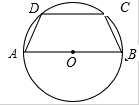 四边形ABCD是⊙O的内接等腰梯形,AB为直径,且AB=4.设∠BOC=θ,ABCD的周长为L.
四边形ABCD是⊙O的内接等腰梯形,AB为直径,且AB=4.设∠BOC=θ,ABCD的周长为L.