题目内容
4.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了五次试验,得到的数据如下,由最小二乘法求得回归方程$\hat y=0.67x+54.9$,现发有一个数据看不清,请你推断出该| 零件个数x | 10 | 20 | 30 | 40 | 50 |
| 加工时间y分钟 | 63 | ? | 75 | 82 | 88 |
分析 根据表中所给的数据,做出横标和纵标的平均数,得到样本中心点,根据由最小二乘法求得回归方程$\widehat{y}$=0.67x+54.9.代入样本中心点求出该数据的值.
解答 解:设表中有一个模糊看不清数据为m.
由表中数据得:$\overline{x}$=30,$\overline{y}$=$\frac{m+308}{5}$,
由于由最小二乘法求得回归方程$\widehat{y}$=0.67x+54.9.
将x=30,y=$\frac{m+308}{5}$代入回归直线方程,得m=67.
故答案为:67.
点评 本题考查线性回归方程的应用,解题的关键是正确应用线性回归方程进行预测.

练习册系列答案
相关题目
14.已知函数f(x)=ax3-3x2+3x,若f'(x)存在唯一的零点x0,且x0>0,则a的值是( )
| A. | 2或1 | B. | 0 | C. | 1或0 | D. | 1 |
9.双曲线9y2-25x2=169的渐近线方程是( )
| A. | y=$\frac{5}{3}$x | B. | y=$\frac{3}{5}$x | C. | y=±$\frac{5}{3}$x | D. | y=±$\frac{3}{5}$x |
16.已知椭圆的方程为$\frac{x^2}{6}+\frac{y^2}{2}=1$,A是其右顶点,B是该椭圆在第一象限部分上的一点,且$∠AOB=\frac{π}{4}$,若点C是椭圆上的动点,则$\overrightarrow{OA}•\overrightarrow{BC}$的取值范围为( )
| A. | [-3,3] | B. | [-9,3] | C. | $[-2-\sqrt{3}\;,\;2-\sqrt{3}]$ | D. | $[-3\sqrt{3}\;,\;3]$ |
13.已知圆C:x2+y2=1,点P为直线$\frac{x}{4}$+$\frac{y}{2}$=1上一动点,过点P向圆C引两条切线PA,PB,A,B为切点,则直线AB经过定点( )
| A. | $({\frac{1}{2},\frac{1}{4}})$ | B. | $({\frac{1}{4},\frac{1}{2}})$ | C. | $({\frac{{\sqrt{3}}}{4},0})$ | D. | $({0,\frac{{\sqrt{3}}}{4}})$ |
14.已知抛物线关于x轴对称,它的顶点在坐标原点O,焦点为F,并且经过点M(2,y0).若点M到该抛物线焦点的距离为3,则△MOF的面积为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |

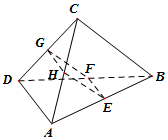 (文科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,
(文科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点, 如图一个水平放置的无盖透明的正方体容器,高12cm,将一个球放在容器口,在向容器内注水,当球面恰好接触水面时测得水深为8cm,如果不计容器厚度,则球的体积为$\frac{2197π}{6}$cm3.
如图一个水平放置的无盖透明的正方体容器,高12cm,将一个球放在容器口,在向容器内注水,当球面恰好接触水面时测得水深为8cm,如果不计容器厚度,则球的体积为$\frac{2197π}{6}$cm3.