题目内容
16.已知椭圆的方程为$\frac{x^2}{6}+\frac{y^2}{2}=1$,A是其右顶点,B是该椭圆在第一象限部分上的一点,且$∠AOB=\frac{π}{4}$,若点C是椭圆上的动点,则$\overrightarrow{OA}•\overrightarrow{BC}$的取值范围为( )| A. | [-3,3] | B. | [-9,3] | C. | $[-2-\sqrt{3}\;,\;2-\sqrt{3}]$ | D. | $[-3\sqrt{3}\;,\;3]$ |
分析 求得直线OB的斜率,代入椭圆方程,求得B点坐标,设C点坐标,利用向量数量积的坐标运算及余弦函数的性质,即可求得$\overrightarrow{OA}•\overrightarrow{BC}$的取值范围.
解答 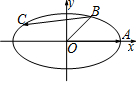 解:由椭圆的方程为$\frac{x^2}{6}+\frac{y^2}{2}=1$焦点在x轴上,A点坐标为($\sqrt{6}$,0),∵$∠AOB=\frac{π}{4}$,
解:由椭圆的方程为$\frac{x^2}{6}+\frac{y^2}{2}=1$焦点在x轴上,A点坐标为($\sqrt{6}$,0),∵$∠AOB=\frac{π}{4}$,
∴直线OB所在的直线为:y=x,
设B点坐标为(x,x),(x>0)
将B点坐标代入到椭圆方程$\frac{x^2}{6}+\frac{y^2}{2}=1$,解得:x2=$\frac{3}{2}$,则x=$\frac{\sqrt{6}}{2}$,
∴B点坐标为($\frac{\sqrt{6}}{2}$,$\frac{\sqrt{6}}{2}$)
设C点坐标为($\sqrt{6}$cosθ,$\sqrt{2}$sinθ),
则$\overrightarrow{OA}•\overrightarrow{BC}$=($\sqrt{6}$,0)•($\sqrt{6}$cosθ-$\frac{\sqrt{6}}{2}$,$\sqrt{2}$sinθ-$\frac{\sqrt{6}}{2}$)=6cosθ-3,
∵cosθ∈[-1,1],
∴当cosθ=-1时,取最小值,最小值为-6-3=-9,
当cosθ=1时,$\overrightarrow{OA}•\overrightarrow{BC}$取最大值,最大值为6-3=3,
$\overrightarrow{OA}•\overrightarrow{BC}$的取值范围[-9,3].
故选B.
点评 本题考查椭圆的参数方程,向量数量积的坐标运算,余弦函数的性质,考查计算能力,属于中档题.

 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | 4 | B. | 8 | C. | 16 | D. | 64 |
| 零件个数x | 10 | 20 | 30 | 40 | 50 |
| 加工时间y分钟 | 63 | ? | 75 | 82 | 88 |
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | {-1,0,1} | B. | {-1,0} | C. | {-2,-1,0} | D. | {0,1,2} |
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | b<c<a |
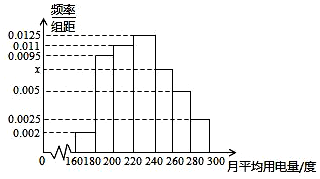 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.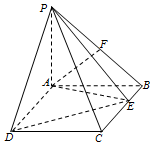 如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=2,AD=4,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=2,AD=4,点F是PB的中点,点E在边BC上移动.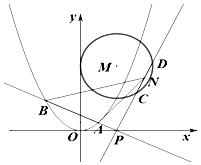 如图,抛物线E:x2=2py(p>0)的焦点为(0,1),圆心M在射线y=2x(x≥0)上且半径为2的圆M与y轴相切.
如图,抛物线E:x2=2py(p>0)的焦点为(0,1),圆心M在射线y=2x(x≥0)上且半径为2的圆M与y轴相切.