题目内容
19. 如图一个水平放置的无盖透明的正方体容器,高12cm,将一个球放在容器口,在向容器内注水,当球面恰好接触水面时测得水深为8cm,如果不计容器厚度,则球的体积为$\frac{2197π}{6}$cm3.
如图一个水平放置的无盖透明的正方体容器,高12cm,将一个球放在容器口,在向容器内注水,当球面恰好接触水面时测得水深为8cm,如果不计容器厚度,则球的体积为$\frac{2197π}{6}$cm3.
分析 根据图形的性质,求出截面圆的半径,即而求出求出球的半径,得出体积
解答 解:根据几何意义得出:边长为12的正方形,球的截面圆为正方形的内切圆,
∴圆的半径为:6,
∵球面恰好接触水面时测得水深为8cm,
∴d=12-8=4,
∴球的半径为:R=$\sqrt{(R-4)^{2}+{6}^{2}}$,
R=$\frac{13}{2}$
∴球的体积为$\frac{4}{3}$π×($\frac{13}{2}$)3=$\frac{2197π}{6}$cm3
故答案为:$\frac{2197π}{6}$
点评 本题考查了球的几何性质,球的体积,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
9.下列命题正确的是( )
| A. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | B. | 若|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,则$\overrightarrow{a}$>$\overrightarrow{b}$ | C. | 若$\overrightarrow{a}$=$\overrightarrow{b}$,则$\overrightarrow{a}$∥$\overrightarrow{b}$ | D. | 若|$\overrightarrow{a}$|=0,则$\overrightarrow{a}$=0 |
10.若某个扇形的半径为3cm,弧长为πcm,则该扇形的面积为( )
| A. | πcm2 | B. | $\frac{3}{2}π$cm2 | C. | 3πcm2 | D. | 6πcm2 |
14.已知两正数x,y 满足x+y=1,则z=$(x+\frac{1}{x})(y+\frac{1}{y})$的最小值为( )
| A. | $\frac{33}{4}$ | B. | $\frac{25}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{{\sqrt{17}}}{4}$ |
4.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了五次试验,得到的数据如下,由最小二乘法求得回归方程$\hat y=0.67x+54.9$,现发有一个数据看不清,请你推断出该
数据的值为67.
| 零件个数x | 10 | 20 | 30 | 40 | 50 |
| 加工时间y分钟 | 63 | ? | 75 | 82 | 88 |
11.a、b均为实数,则a<b<0是a2>b2的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.已知集合A={-2,-1,0,1,2},∁RB={x|$\frac{x-1}{x+2}$≥0},则A∩B=( )
| A. | {-1,0,1} | B. | {-1,0} | C. | {-2,-1,0} | D. | {0,1,2} |
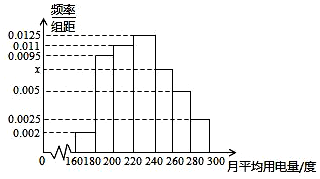 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.