题目内容
14.已知抛物线关于x轴对称,它的顶点在坐标原点O,焦点为F,并且经过点M(2,y0).若点M到该抛物线焦点的距离为3,则△MOF的面积为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
分析 根据点M(2,y0)到该抛物线焦点的距离为3,利用抛物线的定义,可求抛物线方程,进而可得点M的坐标,由此可求△MOF的面积.
解答 解:由题意,抛物线关于x轴对称,开口向右,设方程为y2=2px(p>0)
∵点M(2,y0)到该抛物线焦点的距离为3,
∴2+$\frac{p}{2}$=3,
∴p=2,
∴抛物线方程为y2=4x
∵M(2,y0)
∴y02=8
∴△MOF的面积为$\frac{1}{2}×1×2\sqrt{2}$=$\sqrt{2}$,
故选B.
点评 本题考查抛物线的性质,考查抛物线的定义,解题的关键是利用抛物线的定义求出抛物线方程.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
4.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了五次试验,得到的数据如下,由最小二乘法求得回归方程$\hat y=0.67x+54.9$,现发有一个数据看不清,请你推断出该
数据的值为67.
| 零件个数x | 10 | 20 | 30 | 40 | 50 |
| 加工时间y分钟 | 63 | ? | 75 | 82 | 88 |
5.已知a=-2${\;}^{1-lo{g}_{2}3}$,b=1-log23,c=cos$\frac{5π}{6}$,则a,b,c的大小关系是( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | b<c<a |
4.设实数a,b满足|a|>|b|,则“a-b>0”是“a+b>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
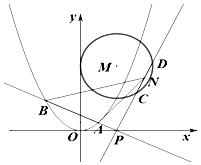 如图,抛物线E:x2=2py(p>0)的焦点为(0,1),圆心M在射线y=2x(x≥0)上且半径为2的圆M与y轴相切.
如图,抛物线E:x2=2py(p>0)的焦点为(0,1),圆心M在射线y=2x(x≥0)上且半径为2的圆M与y轴相切.