题目内容
已知函数y=f(x)是定义域为R的偶函数.当x≥0时,f(x)=
,若关于x的方程[f(x)]2+a•f(x)+b=0(a、b∈R)有且只有7个不同实数根,则实数a的取值范围是 .
|
考点:分段函数的应用
专题:函数的性质及应用
分析:确定函数f(x)的性质,可得关于x的方程[f(x)]2+a•f(x)+b=0(a、b∈R)有且只有7个不同实数根,则方程t2+at+b=0必有两个根t1,t2,其中t1=1,t2∈(
,1),根据根与系数之间的关系,即可得出结论.
| 1 |
| 4 |
解答:
解:由题意,f(x)在(-∞,-2]和[0,2]上是减函数,在[-2,0]和[2,+∞)上是增函数,
∴x=0时,函数取极大值1,x=±2时,取极小值
,
|x|≥16时,f(x)≥1,
∴关于x的方程[f(x)]2+a•f(x)+b=0(a、b∈R)有且只有7个不同实数根,
设t=f(x),
则方程t2+at+b=0必有两个根t1,t2,其中t1=1,t2∈(
,1),
t1+t2=-a∈(
,2),
则-2<a<-
a∈(-2,-
),
故答案为:-2<a<-
.
∴x=0时,函数取极大值1,x=±2时,取极小值
| 1 |
| 4 |

|x|≥16时,f(x)≥1,
∴关于x的方程[f(x)]2+a•f(x)+b=0(a、b∈R)有且只有7个不同实数根,
设t=f(x),
则方程t2+at+b=0必有两个根t1,t2,其中t1=1,t2∈(
| 1 |
| 4 |
t1+t2=-a∈(
| 5 |
| 4 |
则-2<a<-
| 5 |
| 4 |
a∈(-2,-
| 5 |
| 4 |
故答案为:-2<a<-
| 5 |
| 4 |
点评:本题考查分段函数的应用,考查函数的性质,考查数形结合的数学思想,正确理解函数的性质是关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
函数f(x)=
-2sinπx在区间[-2,4]上的所有零点之和等于( )
| 1 |
| 1-x |
| A、2 | B、6 | C、8 | D、10 |
已知不等式组
,表示的三角形区域为M,过该区域三顶点的圆内部记为N,在N中随机取一点,则该点取自区域M的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
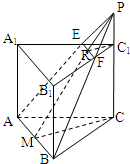 已知正三棱柱ABC-A1B1C1底面边长是10,高是12,过底面一边AB,作与底面ABC成60°角的截面面积是
已知正三棱柱ABC-A1B1C1底面边长是10,高是12,过底面一边AB,作与底面ABC成60°角的截面面积是 正三角形ABC,点M,N,P分别为AB,BC,AC中点,沿MN,MP,NP折起,使A,B,C三点重合后为Q,则折起后二面角Q-MN-P的余弦值为
正三角形ABC,点M,N,P分别为AB,BC,AC中点,沿MN,MP,NP折起,使A,B,C三点重合后为Q,则折起后二面角Q-MN-P的余弦值为