题目内容
已知随机变量X的分布列是
则DX= .
| X | 0 | 1 | 2 |
| P | t | 0.4 | t |
考点:离散型随机变量及其分布列
专题:概率与统计
分析:由随机变量X的分布列示出t=0.3,由此求出EX=1,从而能求出DX的值.
解答:
解:由题意知t+0.4+t=1,解得t=0.3,
EX=0×0.3+1×0.4+2×0.3=1,
∴DX=(0-1)2×0.3+(1-1)2×0.4+(2-1)2×0.3=0.6.
故答案为:0.6.
EX=0×0.3+1×0.4+2×0.3=1,
∴DX=(0-1)2×0.3+(1-1)2×0.4+(2-1)2×0.3=0.6.
故答案为:0.6.
点评:本题考查离散型随机变量的方差的求法,是基础题,解题时要认真审题,注意随机变量的分布列的性质的合理运用.

练习册系列答案
相关题目
函数f(x)=
-2sinπx在区间[-2,4]上的所有零点之和等于( )
| 1 |
| 1-x |
| A、2 | B、6 | C、8 | D、10 |
 如图所示,用边长为60cm的正方形铁皮做一个无盖水箱,先在四角分别截去一个相同的小正方形,然后把四边翻折90°角,再焊接成无盖水箱,则水箱的最大容积为
如图所示,用边长为60cm的正方形铁皮做一个无盖水箱,先在四角分别截去一个相同的小正方形,然后把四边翻折90°角,再焊接成无盖水箱,则水箱的最大容积为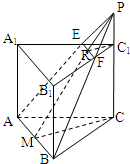 已知正三棱柱ABC-A1B1C1底面边长是10,高是12,过底面一边AB,作与底面ABC成60°角的截面面积是
已知正三棱柱ABC-A1B1C1底面边长是10,高是12,过底面一边AB,作与底面ABC成60°角的截面面积是