题目内容
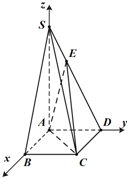
如图所示,直角梯形PBCD,PD∥BC,∠D=90°,PD=9,BC=3,CD=4,点A在PD上,且PA=2AD,将△PAB沿AB折到△SAB的位置,使SB⊥BC.

(Ⅰ)求证:SA⊥AD;
(Ⅱ)点E在SD上,且
=
,求二面角S-AC-E的余弦值.

(Ⅰ)求证:SA⊥AD;
(Ⅱ)点E在SD上,且
| SE |
| 1 |
| 3 |
| SD |
考点:用空间向量求平面间的夹角,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知条件推导出四边形ABCD为矩形,AB⊥BC,由SB⊥BC,得BC⊥平面SAB,由此能证明SA⊥AD.
(Ⅱ)由题意以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,利用向量法能求出二面角D-BE-C的余弦值.
(Ⅱ)由题意以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,利用向量法能求出二面角D-BE-C的余弦值.
解答:
 (本小题满分12分)
(本小题满分12分)
(Ⅰ)证明:∵PD=9,PA=2AD,∴PA=6,AD=3,
又∵BC=3,AD∥BC,∠D=90°,
∴四边形ABCD为矩形,AB⊥BC,…(2分)
又∵SB⊥BC,AB∩SB=B,故BC⊥平面SAB,…(4分)
从而BC⊥SA,又因为BC∥AD,所以SA⊥AD.…(6分)
(Ⅱ)解:由题意和( I)知SA⊥AB,SA⊥AD,AB⊥AD,
∴以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,
则A(0,0,0),B(4,0,0),C(4,3,0),D(0,3,0),S(0,0,6),
从而
=(0,0,6),
=(4,3,0),
=(0,3,-6)
由
=
,
知
=
+
=
+
=(0,0,6)+
×(0,3,-6)=(0,1,4).…(8分)
设平面AEC的法向量为
=(x1,y1,z1),
则
,即
,
令z1=1,则x1=3,y1=-4,可取
=(3,-4,1),
设平面SAC的法向量为
=(x2,y2,z2),
则
,即
,
令x2=3,则y2=-4,z2=0,可取
=(3,-4,0),…(10分)
∴cos<
,
>=
=
=
,
故二面角D-BE-C的余弦值为
.…(12分)
 (本小题满分12分)
(本小题满分12分)(Ⅰ)证明:∵PD=9,PA=2AD,∴PA=6,AD=3,
又∵BC=3,AD∥BC,∠D=90°,
∴四边形ABCD为矩形,AB⊥BC,…(2分)
又∵SB⊥BC,AB∩SB=B,故BC⊥平面SAB,…(4分)
从而BC⊥SA,又因为BC∥AD,所以SA⊥AD.…(6分)
(Ⅱ)解:由题意和( I)知SA⊥AB,SA⊥AD,AB⊥AD,
∴以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,
则A(0,0,0),B(4,0,0),C(4,3,0),D(0,3,0),S(0,0,6),
从而
| AS |
| AC |
| SD |
由
| SE |
| 1 |
| 3 |
| SD |
知
| AE |
| AS |
| SE |
| AS |
| 1 |
| 3 |
| SD |
| 1 |
| 3 |
设平面AEC的法向量为
| m |
则
|
|
令z1=1,则x1=3,y1=-4,可取
| m |
设平面SAC的法向量为
| n |
则
|
|
令x2=3,则y2=-4,z2=0,可取
| n |
∴cos<
| m |
| n |
| ||||
|
|
| 25 | ||
5
|
5
| ||
| 26 |
故二面角D-BE-C的余弦值为
5
| ||
| 26 |
点评:本题考查异面直线垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在直平行六面体ABCD-A1B1C1D1中,侧棱AA1=3,AB=3,BC=
如图,在直平行六面体ABCD-A1B1C1D1中,侧棱AA1=3,AB=3,BC=