题目内容
已知函数f(x)=cosx•sin(
-x).
(Ⅰ)求f(
)的值;
(Ⅱ)求使4f(x)<1成立的x的取值集合.
| 5π |
| 6 |
(Ⅰ)求f(
| π |
| 3 |
(Ⅱ)求使4f(x)<1成立的x的取值集合.
考点:两角和与差的正弦函数,三角函数中的恒等变换应用
专题:三角函数的求值
分析:(Ⅰ)根据函数 f(x)的解析式,直接求得f(
)的值.
(Ⅱ)利用三角恒等变换化简函数的解析式为f(x)=
+
cos(2x-
),要解的不等式即
cos(2x-
)<0,令2kπ+
<2x-
<2kπ+
,k∈z,求得x的范围,即为所求.
| π |
| 3 |
(Ⅱ)利用三角恒等变换化简函数的解析式为f(x)=
| 1 |
| 4 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解答:
解:(Ⅰ)∵f(x)=cosx•sin(
-x),∴f(
)=cos
sin
=
×1=
.
(Ⅱ)∵f(x)=cosx•sin(
-x)=cosx(
cosx+
sinx)
=
•
+
sin2x=
+
cos(2x-
),
∴4f(x)<1即
cos(2x-
)<0,∴2kπ+
<2x-
<2kπ+
,k∈z.
解得 kπ+
<x<kπ+
,
∴使4f(x)<1成立的x的取值集合为 {x|kπ+
<x<kπ+
,k∈z}.
| 5π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)∵f(x)=cosx•sin(
| 5π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
=
| 1 |
| 2 |
| 1+cos2x |
| 2 |
| ||
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| π |
| 3 |
∴4f(x)<1即
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解得 kπ+
| 5π |
| 12 |
| 11π |
| 12 |
∴使4f(x)<1成立的x的取值集合为 {x|kπ+
| 5π |
| 12 |
| 11π |
| 12 |
点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的单调性,属于中档题.

练习册系列答案
相关题目
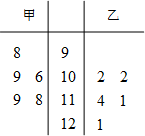 在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如茎叶图所示:
在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如茎叶图所示: 如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD.AB=AD=
如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD.AB=AD=