题目内容
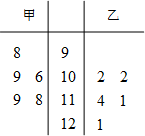 在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如茎叶图所示:
在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如茎叶图所示:(Ⅰ)从甲、乙两人中选择1人参加数学趣味知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(Ⅱ) 从乙的5次培训成绩中随机选择2个,记被抽到的分数超过110分的个数为ξ,试求ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差,众数、中位数、平均数,极差、方差与标准差
专题:应用题,概率与统计
分析:(Ⅰ)求出
=
,
>
,可知甲和乙成绩的平均水平一样,乙的方差小,乙发挥比甲稳定;
(Ⅱ)ξ可能取值为0,1,2,求出相应的概率,可计算出ξ的分布列及数学期望.
. |
| x甲 |
. |
| x乙 |
| s | 2 甲 |
| s | 2 乙 |
(Ⅱ)ξ可能取值为0,1,2,求出相应的概率,可计算出ξ的分布列及数学期望.
解答:
解:(Ⅰ)甲、乙两人的平均成绩分别是
=
(98+106+109+118+119)=110,
=
(102+102+111+114+121)=110,.…(2分)
甲、乙两人成绩的方差分别是
=
[(98-110)2+(106-110)2+(109-110)2+(118-110)2+(119-110)2]=
,
=
[(102-110)2+(102-110)2+(111-110)2+(114-110)2+(121-110)2]=
.(4分)
由
=
,
>
,可知甲和乙成绩的平均水平一样,乙的方差小,乙发挥比甲稳定,
故选择乙.…(6分)
(Ⅱ)ξ可以取0,1,2.…(7分)
P(ξ=0)=
=
;…(8分)P(ξ=1)=
=
=
;…(9分)P(ξ=2)=
=
.…(10分)
ξ的分布列为
…(11分)
期望Eξ=0×
+1×
+2×
=
.…(12分)
. |
| x甲 |
| 1 |
| 5 |
. |
| x乙 |
| 1 |
| 5 |
甲、乙两人成绩的方差分别是
| s | 2 甲 |
| 1 |
| 5 |
| 306 |
| 5 |
| s | 2 乙 |
| 1 |
| 5 |
| 266 |
| 5 |
由
. |
| x甲 |
. |
| x乙 |
| s | 2 甲 |
| s | 2 乙 |
故选择乙.…(6分)
(Ⅱ)ξ可以取0,1,2.…(7分)
P(ξ=0)=
| ||
|
| 1 |
| 10 |
| ||||
|
| 6 |
| 10 |
| 3 |
| 5 |
| ||
|
| 3 |
| 10 |
ξ的分布列为
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
期望Eξ=0×
| 1 |
| 10 |
| 3 |
| 5 |
| 3 |
| 10 |
| 6 |
| 5 |
点评:本小题主要考查统计知识、离散型随机变量的分布列和数学期望等基础知识,考查数据处理、推理论证、运算求解能力和应用意识.

练习册系列答案
相关题目
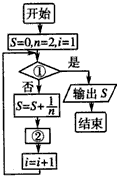 如图给出的是计算
如图给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 108 |
| A、i>108,n=n+1 |
| B、i>108,n=n+2 |
| C、i>54,n=n+2 |
| D、i≤54,n=n+2 |
 如图,P是圆O外一点,过P引圆O的两条割线PAB、PCD,PA=AB=
如图,P是圆O外一点,过P引圆O的两条割线PAB、PCD,PA=AB=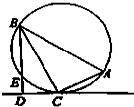 如图,在△ABC中,∠C=90°,∠A=60°,过C作△ABC的外接圆的切线CD,BD⊥CD于D.BD与外接圆交于点E,已知DE=5,则△ABC的外接圆的半径为
如图,在△ABC中,∠C=90°,∠A=60°,过C作△ABC的外接圆的切线CD,BD⊥CD于D.BD与外接圆交于点E,已知DE=5,则△ABC的外接圆的半径为