题目内容
将函数y=sinx的图象向右平移
个单位,再将所得图象上的各点纵坐标保持不变,横坐标变为原来的m(m>0)倍后的函数图象关于直线x=-
对称,则实数m的最大值为( )
| π |
| 3 |
| π |
| 3 |
| A、5 | B、4 | C、3 | D、2 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:根据函数y=Asin(ωx+φ)的图象变换规律,变换后得到函数y=sin(
x-
)的图象.再根据所得图象关于直线x=-
对称,可得
×(-
)-
=kπ+
,k∈z,即 m=
,k∈z,由此求得m的最大值.
| 1 |
| m |
| π |
| 3 |
| π |
| 3 |
| 1 |
| m |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| -2 |
| 6k+5 |
解答:
解:将函数y=sinx的图象向右平移
个单位,可得函数y=sin(x-
)的图象;
再将所得图象上的各点纵坐标保持不变,横坐标变为原来的m(m>0)倍后
得到函数y=sin(
x-
)的图象.
再根据函数y=sin(
x-
)的图象关于直线x=-
对称,可得
×(-
)-
=kπ+
,k∈z,
即 m=
,k∈z,
故m的最大值为
=2,
故选:D.
| π |
| 3 |
| π |
| 3 |
再将所得图象上的各点纵坐标保持不变,横坐标变为原来的m(m>0)倍后
得到函数y=sin(
| 1 |
| m |
| π |
| 3 |
再根据函数y=sin(
| 1 |
| m |
| π |
| 3 |
| π |
| 3 |
| 1 |
| m |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
即 m=
| -2 |
| 6k+5 |
故m的最大值为
| -2 |
| -1 |
故选:D.
点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于中档题.

练习册系列答案
相关题目
在正四面体ABCD中,E、F、G分别是BC、CD、DB的中点,下面四个结论中不正确的是( )
| A、BC∥平面AGF |
| B、EG⊥平面ABF |
| C、平面AEF⊥平面BCD |
| D、平面ABF⊥平面BCD |
满足条件x2+y2≤1的点(x,y)构成的平面区域面积为S1,满足条件[x]2+[y]2≤1的点(x,y)构成的平面区域的面积为S2,其中[x]、[y]分别表示不大于x,y的最大整数,例如:[-0.4]=-1,[1.6]=1,则S1+S2=( )
| A、π+3 | B、π+4 |
| C、π+5 | D、π+6 |
等比数列{an}中a4+a8=-2,则a42+2a62+a6a10的值为( )
| A、4 | B、5 | C、8 | D、-9 |
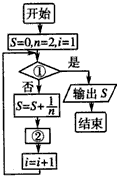 如图给出的是计算
如图给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 108 |
| A、i>108,n=n+1 |
| B、i>108,n=n+2 |
| C、i>54,n=n+2 |
| D、i≤54,n=n+2 |
已知(ax+1)5的展开式中x3的系数是10,则实数a的值是( )
| A、1 | ||
B、
| ||
| C、-1 | ||
| D、2 |