题目内容
调查某电脑公司的三名产品推销员,其工作年限与年推销金额数据如表:由表中数据算出线性回归方程
=bx+a中的b=
,若该电脑公司第四名推销员的工作年限为6年,则估计他的年推销金额为 万元.
| ∧ |
| y |
| 7 |
| 26 |
| 推销员编号 | 1 | 2 | 3 |
| 工作年限x(年) | 3 | 5 | 10 |
| 年推销金额y(万元) | 2 | 3 | 4 |
考点:线性回归方程
专题:概率与统计
分析:根据所给的两组数据,做出x和y的平均数,写出这组数据的样本中心点,根据线性回归方程一定过样本中心点,得到线性回归直线一定过的点的坐标.最后根据第4名推销员的工作年限为6年,即当x=6时,把自变量的值代入线性回归方程,得到y的预报值,即估计出第4名推销员的年推销金额.
解答:
解:由条件可知
=
=6,
=
=3,
代入回归方程,可得a=
,所以
=
x+
,
当x=6 时,
=3,
估计他的年推销金额为3万元.
故答案为:3.
. |
| x |
| 3+5+10 |
| 3 |
. |
| y |
| 2+3+4 |
| 3 |
代入回归方程,可得a=
| 18 |
| 13 |
| ? |
| y |
| 7 |
| 26 |
| 18 |
| 13 |
当x=6 时,
| ? |
| y |
估计他的年推销金额为3万元.
故答案为:3.
点评:本题考查线性回归方程的意义,线性回归方程一定过样本中心点,本题解题的关键是正确求出样本中心点,题目的运算量比较小,是一个基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若sina=
,a是第二象限的角,则cosa=( )
| 4 |
| 5 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
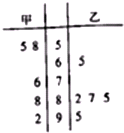 如图是甲、乙两名同学参加“汉字听写大赛”选拔性测试(在相同的测试条件下)5次测试的成绩(单位:分)的茎叶图,设甲乙两名同学的平均分数依次为
如图是甲、乙两名同学参加“汉字听写大赛”选拔性测试(在相同的测试条件下)5次测试的成绩(单位:分)的茎叶图,设甲乙两名同学的平均分数依次为. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知斜三棱柱的三视图如图所示,该斜三棱柱的体积为
已知斜三棱柱的三视图如图所示,该斜三棱柱的体积为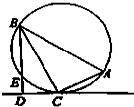 如图,在△ABC中,∠C=90°,∠A=60°,过C作△ABC的外接圆的切线CD,BD⊥CD于D.BD与外接圆交于点E,已知DE=5,则△ABC的外接圆的半径为
如图,在△ABC中,∠C=90°,∠A=60°,过C作△ABC的外接圆的切线CD,BD⊥CD于D.BD与外接圆交于点E,已知DE=5,则△ABC的外接圆的半径为