题目内容
一个几何体的三视图及其尺寸，如图所示，则该几何体的侧面积为（ ）
| A、80 | B、40 | C、48 | D、96 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：先判断三视图复原的几何体的形状，结合三视图的数据，确定斜高，再求侧面积．
解答：
解：三视图复原的几何体是正四棱锥，
斜高是5，底面边长是8，
侧面积为
×4×8×5=80；
故选：A
斜高是5，底面边长是8，
侧面积为
| 1 |
| 2 |
故选：A
点评：本题考查由三视图求几何体的侧面积，考查空间想象能力，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在极坐标系中，点（2，
）到直线ρsin（θ-
）=1的距离是（ ）
| π |
| 6 |
| π |
| 6 |
A、
| ||
| B、3 | ||
| C、1 | ||
| D、2 |
设△ABC的内角A，B，C所对的边分别为a，b，c，若b2+c2＜a2，则△ABC的形状为（ ）
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不确定 |
某医院从五名护士和四名医生中，选出4人组成一个医疗小组，支援抗震救灾活动，若这四人中必须既有护士又有医生，则不同的选法共有（ ）
| A、126 | B、125 |
| C、121 | D、120 |
向量
=（-2，-1），
=（λ，1），若
与
夹角为钝角，则λ取值范围是（ ）
| a |
| b |
| a |
| b |
A、（-
| ||
| B、（2，+∞） | ||
C、（-
| ||
D、（-∞，-
|
设m∈N*，且m＜15，则（15-m）（16-m）…（20-m）等于（ ）
A、A
| ||
B、A
| ||
C、A
| ||
D、A
|
已知双曲线my2-x2=1（m∈R）与椭圆
+x2=1有相同的焦点，则该双曲线的渐近线方程为（ ）
| y2 |
| 5 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
| D、y=±3x |
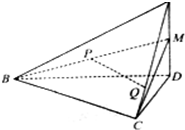在四面体A-BCD中，AD⊥平面BCD，BC⊥CD，∠DBC=30°，AD=2，BD=2