题目内容
某医院从五名护士和四名医生中,选出4人组成一个医疗小组,支援抗震救灾活动,若这四人中必须既有护士又有医生,则不同的选法共有( )
| A、126 | B、125 |
| C、121 | D、120 |
考点:计数原理的应用
专题:排列组合
分析:利用间接法,从五名护士和四名医生中,选出4人组成一个医疗小组,然后排除只有只有护士参加和只有医生参加的,问题得以解决.
解答:
解:利用间接法,从五名护士和四名医生中,选出4人组成一个医疗小组,有
种,只有护士参加的有
,只有医生参加的有
,
故这四人中必须既有护士又有医生,则不同的选法共有
-
-
=121.
故选:C.
| C | 4 9 |
| C | 4 5 |
| C | 4 4 |
故这四人中必须既有护士又有医生,则不同的选法共有
| C | 4 9 |
| C | 4 5 |
| C | 4 4 |
故选:C.
点评:本题考查了组合问题,间接法是常用的方法,属于基础题.

练习册系列答案
相关题目
为防止灰太狼的入侵,确保小羊安全,慢羊羊村长对羊村大门设置了“一次一密”的密码保护模式:它使用了四个不同的口令A,B,C,D,但每次只能使用其中的一种,且每次都是从上次未使用的三个口令中等可能地随机选用一种.设第1次使用C口令,那么第6次也使用C口令的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列式子中不能表示函数y=f(x)的是( )
| A、x=y2+1 | ||
| B、y=2x2+1 | ||
| C、x-2y=6 | ||
D、x=
|
如图,不等式x2-y2-4x-2y+3≥0表示的平面区域是( )
A、 |
B、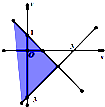 |
C、 |
D、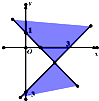 |
求
的值( )
| 4 | (3-π)4 |
| A、0 | B、3-π | C、π-3 | D、无解 |
一个几何体的三视图及其尺寸,如图所示,则该几何体的侧面积为( )


| A、80 | B、40 | C、48 | D、96 |
设Sn是数列{an}的前n项和,且Sn=n2,则{an}是( )
| A、只是等比数列 |
| B、只是等差数列 |
| C、既是等比,又是等差数列 |
| D、既非等比,又非等差数列 |