题目内容
函数y=log
(1+λcosx)的最小值是-2,则λ的值是 .
| 1 |
| 2 |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:t=1+λcosx,0<t≤1+|λ|,根据单调性确定y=log
t,的最小值为log
(1+|t|),即可得出-2=log
(1+|t|),
求解即可得出λ的值.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
求解即可得出λ的值.
解答:
解:函数y=log
(1+λcosx)t=1+λcosx,0<t≤1+|λ|,
∴y=log
t,0<t≤1+|λ|,单调递减函数,
∴y=log
t,的最小值为log
(1+|t|),
∵最小值是-2,
∴-2=log
(1+|t|),
∴|λ|=3,λ=±3
故答案为:±3
| 1 |
| 2 |
∴y=log
| 1 |
| 2 |
∴y=log
| 1 |
| 2 |
| 1 |
| 2 |
∵最小值是-2,
∴-2=log
| 1 |
| 2 |
∴|λ|=3,λ=±3
故答案为:±3
点评:本题考查了复合函数的单调性,三角函数,对数函数的性质,运算,属于中档题.

练习册系列答案
相关题目
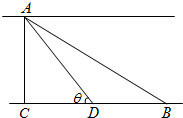 如图,一条河的两岸是平行线,两岸边各有一个小镇A与B,它们的直线距离为2km,河宽AC=1km,根据规划,需要在两岸间铺设一条电缆线,从A处铺设水下电缆到D处(D为线段BC上的点),再从D处铺设地下电缆到B处,已知铺设水下电缆的费用是铺设地下电缆费用的2倍,记∠ADC=θ.
如图,一条河的两岸是平行线,两岸边各有一个小镇A与B,它们的直线距离为2km,河宽AC=1km,根据规划,需要在两岸间铺设一条电缆线,从A处铺设水下电缆到D处(D为线段BC上的点),再从D处铺设地下电缆到B处,已知铺设水下电缆的费用是铺设地下电缆费用的2倍,记∠ADC=θ.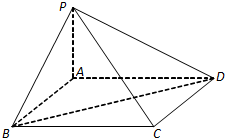 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且PB=PD.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且PB=PD.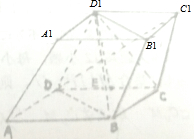 如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为a的正方形,D1是底面ABCD上的射影E恰好是CD的中点,BD1⊥DC1.
如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为a的正方形,D1是底面ABCD上的射影E恰好是CD的中点,BD1⊥DC1.