题目内容
 如图,A是双曲线
如图,A是双曲线| x2 |
| 4 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:直线AM的斜率为k(k>0,k≠±
,k≠±2),方程为y=k(x-2),代入
-y2=1,求出M的坐标,同理得N的坐标,分类讨论,即可得出结论.
| 1 |
| 2 |
| x2 |
| 4 |
解答:
解:设直线AM的斜率为k(k>0,k≠±
,k≠±2),方程为y=k(x-2),
代入
-y2=1,可得M(
,
),
同理得N(
,-
)
当k=±1时,xM=xN=
,所以过(
,0)(8分)
当k≠±1,k≠±
,k≠±2时,由直线MN的方程得,y=k′(x-
) (10分)
所以,直线MN过x轴上的定点(
,0). (14分)
| 1 |
| 2 |
代入
| x2 |
| 4 |
| 8k2+2 |
| 4k2-1 |
| 4k |
| 4k2-1 |
同理得N(
| 2k2+8 |
| 4-k2 |
| 4k |
| 4-k2 |
当k=±1时,xM=xN=
| 10 |
| 3 |
| 10 |
| 3 |
当k≠±1,k≠±
| 1 |
| 2 |
| 10 |
| 3 |
所以,直线MN过x轴上的定点(
| 10 |
| 3 |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了考生分析推理和基本的运算能力,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
已知集合A={1,2,3,4,5,6},在A中任取三个元素,使它们的和小于余下的三个元素的和,则取法种数共有( )
| A、4 | B、10 | C、15 | D、20 |
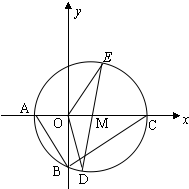 如图,△ABC中,
如图,△ABC中,