题目内容
由数字0,1,2,3组成一个没有重复数字,且不被10整除的四位数,则两个偶数不相邻的概率是 .
考点:列举法计算基本事件数及事件发生的概率,等可能事件的概率,排列、组合及简单计数问题
专题:计算题,概率与统计
分析:根据题意,列出所有的情况共18个,其中不被10整除的四位数是满足个位数不为0的共有12个,满足两个偶数不相邻的基本事件有4个,根据古典概型的概率计算公式可得结论.
解答:
解:根据题意,列出所有的情况1023,1032,1203,1230,1302,1320,2013,2031,2103,2130,2301,2310,3012,3021,3102,3120,3201,3210共18个,
其中不被10整除的四位数是满足个位数不为0的共有12个,即该实验所有的基本事件1023,1032,1203,1302,2013,2031,2103,2301,3012,3021,3102,3201,共12个,
则满足两个偶数不相邻的基本事件有4个,
根据古典概型的概率计算公式可得P=
.
故答案为:
.
其中不被10整除的四位数是满足个位数不为0的共有12个,即该实验所有的基本事件1023,1032,1203,1302,2013,2031,2103,2301,3012,3021,3102,3201,共12个,
则满足两个偶数不相邻的基本事件有4个,
根据古典概型的概率计算公式可得P=
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查古典概型,考查列举法的运用,确定基本事件的个数是关键,属于中档题.

练习册系列答案
相关题目
如图所示的程序框图输出的结果是S=720,则判断框内应填的条件是( )

| A、i≤7 | B、i>7 |
| C、i≤9 | D、i>9 |
已知两条直线m,n和平面α,且m在α内,n在α外,则“n∥α”是“m∥n”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
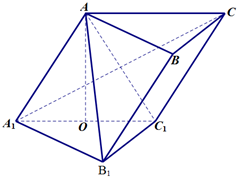 如图,在斜三棱柱ABC-A1B1C1中,点O是A1C1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.
如图,在斜三棱柱ABC-A1B1C1中,点O是A1C1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2. 如图,A是双曲线
如图,A是双曲线