题目内容
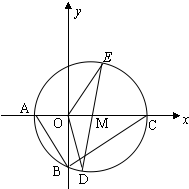 如图,△ABC中,∠B=
如图,△ABC中,∠B=| π |
| 2 |
| 2 |
(1)求圆M的标准方程;
(2)若点O为坐标原点,DE是圆M的任意一条直径,试问
| OD |
| OE |
考点:直线与圆锥曲线的综合问题
专题:直线与圆
分析:(1)在Rt△ABC中,由射影定理求得AC的长,则M点坐标可求,圆M的方程可求;
(2)设出过M的直线方程,和圆的方程联立后化为关于y的一元二次方程,由根与系数关系得到D、E两点的纵坐标的和与积,代入数量积公式求得
•
为定值.
(2)设出过M的直线方程,和圆的方程联立后化为关于y的一元二次方程,由根与系数关系得到D、E两点的纵坐标的和与积,代入数量积公式求得
| OD |
| OE |
解答:
解:(1)在△ABC中,∵∠B=
,OA=2,OB=2
,
∴AB=
=2
,
又AB2=AO•AC,
∴AC=
=
=6,
∴M(1,0),圆M的半径为3,
则圆M:(x-1)2+y2=9;
(2)设过M的直线为:x=my+1与圆(x-1)2+y2=9的两个交点为D(x1,y1),E(x2,y2),
联立
,
得:(m2+1)y2=9.
∴y1+y2=0,y1y2=
,
则
•
=x1x2+y1y2=(my1+1)(my2+1)+y1y2
=(m2+1)y1y2+m(y1+y2)+1=-8,
当过M的直线垂直于y轴时,经检验满足.
∴
•
=-8,为定值.
| π |
| 2 |
| 2 |
∴AB=
22+(2
|
| 3 |
又AB2=AO•AC,
∴AC=
| AB2 |
| AO |
| 12 |
| 2 |
∴M(1,0),圆M的半径为3,
则圆M:(x-1)2+y2=9;
(2)设过M的直线为:x=my+1与圆(x-1)2+y2=9的两个交点为D(x1,y1),E(x2,y2),
联立
|
得:(m2+1)y2=9.
∴y1+y2=0,y1y2=
| -9 |
| m2+1 |
则
| OD |
| OE |
=(m2+1)y1y2+m(y1+y2)+1=-8,
当过M的直线垂直于y轴时,经检验满足.
∴
| OD |
| OE |
点评:本题考查了圆的方程的求法,训练了平面向量数量积的坐标运算,是中档题.

练习册系列答案
相关题目
已知一个算法,其流程图如图,则输出的结果是( )


| A、10 | B、11 | C、8 | D、9 |
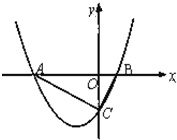 如图,已知抛物线
如图,已知抛物线 如图,A是双曲线
如图,A是双曲线