题目内容
已知抛物线y2=8x过点M(4,2)的直线l与抛物线相交于A(x1,y1),B(x2,y2)两点,当y12+y22取得最小值时,直线l的方程是 .
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:求出直线l的斜率不存在时的y12+y22的值,然后写出直线l的斜率存在时的方程,和抛物线方程联立后化为关于y的一元二次方程,写出根与系数关系,通过配方变形把y12+y22用y1+y2,y1y2表示,代入根与系数关系后化为关于
的一元二次方程,由此求得最小值及取得最小值时的k值,则直线方程可求.
| 1 |
| k |
解答:
解:当直线l的斜率不存在时,直线l的方程为x=4,
代入y2=8x,得y2=32,
∴y12+y22=2y2=64;
当直线l的斜率存在时,
设直线l的方程为y-2=k(x-4)(k≠0),
即x=
-
+4,
代入y2=8x得:y2=8(
-
+4),
整理得:y2-
y+
-32=0.
y1+y2=
,y1y2=
-32.
∴y12+y22=(y1+y2)2-2y1y2=(
)2-2(
-32)=
-
+64.
∴当
=
=
,即k=4时,(y12+y22)min=60.
综上,当k=4时,y12+y22取得最小值.
∴当y12+y22取得最小值时,直线l的方程是y-2=4(x-4).
即4x-y-14=0.
故答案为:4x-y-14=0.
代入y2=8x,得y2=32,
∴y12+y22=2y2=64;
当直线l的斜率存在时,
设直线l的方程为y-2=k(x-4)(k≠0),
即x=
| y |
| k |
| 2 |
| k |
代入y2=8x得:y2=8(
| y |
| k |
| 2 |
| k |
整理得:y2-
| 8 |
| k |
| 16 |
| k |
y1+y2=
| 8 |
| k |
| 16 |
| k |
∴y12+y22=(y1+y2)2-2y1y2=(
| 8 |
| k |
| 16 |
| k |
| 64 |
| k2 |
| 32 |
| k |
∴当
| 1 |
| k |
| 32 |
| 2×64 |
| 1 |
| 4 |
综上,当k=4时,y12+y22取得最小值.
∴当y12+y22取得最小值时,直线l的方程是y-2=4(x-4).
即4x-y-14=0.
故答案为:4x-y-14=0.
点评:本题考查抛物线的应用,考查了分类讨论的数学思想方法,灵活运用韦达定理和灵活配方变形是解答该题的关键,训练了二次函数最值的求法.是中档题.

练习册系列答案
相关题目
已知一个算法,其流程图如图,则输出的结果是( )


| A、10 | B、11 | C、8 | D、9 |
 如图,A是双曲线
如图,A是双曲线
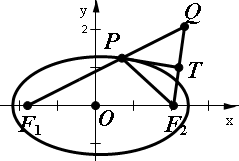 已知椭圆
已知椭圆