题目内容
已知函数f(x)=(2-a)(x-1)-2lnx,g(x)=ex-x-b.(a为常数,e为自然对数的底,e≈2.71828)
(Ⅰ)当a=1时,①求f(x)的单调区间;②若对任意的X1∈R*,存在x2∈R,使f(x1)≥g(x2),求实数b的取值范围;
(Ⅱ)若函数f(x)在区间(0,
)上无零点,求a的最小值.
(Ⅰ)当a=1时,①求f(x)的单调区间;②若对任意的X1∈R*,存在x2∈R,使f(x1)≥g(x2),求实数b的取值范围;
(Ⅱ)若函数f(x)在区间(0,
| 1 |
| 2 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:转化思想,导数的综合应用
分析:(1)①求出a=1时f(x)的导数,分别令它大于0、小于0,求出单调区间;②分别求出f(x),g(x)在定义域内的最小值,由题意知:只要f(x)min≥g(x)min,即可求出b的取值范围;
(2)函数f(x)在区间(0,
)上无零点等价于对?x∈(0,
),f(x)>0恒成立,利用参数分离将a分离得:a>2-
,对右边两次求导,得到右边函数在(0,
)上的单调性,从而得到右边的最大值,只要a大于等于它即可.
(2)函数f(x)在区间(0,
| 1 |
| 2 |
| 1 |
| 2 |
| 2lnx |
| x-1 |
| 1 |
| 2 |
解答:
解:(Ⅰ)①当a=1时,f(x)=x-1-2lnx(x>0)则f′(x)=1-
,
令f′(x)>0得x>2,令f′(x)<0得0<x<2,
故f(x)的单调递减区间为(0,2),单调递增区间为(2,+∞);
②g(x)=ex-x-b 则g′(x)=ex-1,
当x>0时,g′(x)>0,即g(x)在(0,+∞)上单调递增,
当x<0时,g′(x)<0,即g(x)在(-∞,0)上单调递减,
则g(x)min=g(0)=1-b;由①易知函数f(x)min=1-2ln2,
若对任意的x1∈R+,存在x2∈R,使f(x1)≥g(x2),
只需f(x)min≥g(x)min,即1-2ln2≥1-b,所以b≥2ln2;
(Ⅱ)∵函数f(x)<0在区间(0,
)上不可能恒成立,
故要使函数f(x)在区间(0,
)上无零点,只要对?x∈(0,
),f(x)>0恒成立.
即对?x∈(0,
),a>2-
恒成立,
令l(x)=2-
(x∈(0,
))则l′(x)=
=
,
再令m(x)=2lnx+
-2,则m′(x)=
-
=
,
∵x∈(0,
),∴m′(x)<0,
故函数m(x)在区间(0,
)上单调递减,
∴m(x)>m(
)=2-2ln2>0,
即l′(x)>0,∴函数l(x)在区间(0,
)上单调递增,
∴l(x)<l(
)=2-4ln2,
故只要a≥2-4ln2,函数f(x)在区间(0,
)上无零点,
∴amin=2-4ln2.
| 2 |
| x |
令f′(x)>0得x>2,令f′(x)<0得0<x<2,
故f(x)的单调递减区间为(0,2),单调递增区间为(2,+∞);
②g(x)=ex-x-b 则g′(x)=ex-1,
当x>0时,g′(x)>0,即g(x)在(0,+∞)上单调递增,
当x<0时,g′(x)<0,即g(x)在(-∞,0)上单调递减,
则g(x)min=g(0)=1-b;由①易知函数f(x)min=1-2ln2,
若对任意的x1∈R+,存在x2∈R,使f(x1)≥g(x2),
只需f(x)min≥g(x)min,即1-2ln2≥1-b,所以b≥2ln2;
(Ⅱ)∵函数f(x)<0在区间(0,
| 1 |
| 2 |
故要使函数f(x)在区间(0,
| 1 |
| 2 |
| 1 |
| 2 |
即对?x∈(0,
| 1 |
| 2 |
| 2lnx |
| x-1 |
令l(x)=2-
| 2lnx |
| x-1 |
| 1 |
| 2 |
-
| ||
| (x-1)2 |
2lnx+
| ||
| (x-1)2 |
再令m(x)=2lnx+
| 2 |
| x |
| 2 |
| x |
| 2 |
| x2 |
| -2(1-x) |
| x2 |
∵x∈(0,
| 1 |
| 2 |
故函数m(x)在区间(0,
| 1 |
| 2 |
∴m(x)>m(
| 1 |
| 2 |
即l′(x)>0,∴函数l(x)在区间(0,
| 1 |
| 2 |
∴l(x)<l(
| 1 |
| 2 |
故只要a≥2-4ln2,函数f(x)在区间(0,
| 1 |
| 2 |
∴amin=2-4ln2.
点评:本题是导数在函数中的综合应用:求单调区间,求极值,求最值,注意转化思想在解题中的运用,注意分离参数法的运用,转化为求函数最值问题,同时注意二次求导在解题中的运用,以及对“任意”与“存在”词语的理解.

练习册系列答案
相关题目
已知两条直线m,n和平面α,且m在α内,n在α外,则“n∥α”是“m∥n”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
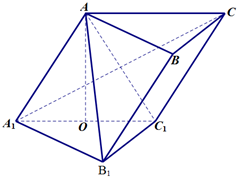 如图,在斜三棱柱ABC-A1B1C1中,点O是A1C1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.
如图,在斜三棱柱ABC-A1B1C1中,点O是A1C1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.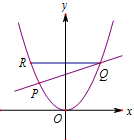 如图,设直线l:y=kx+
如图,设直线l:y=kx+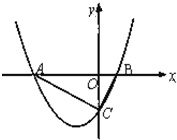 如图,已知抛物线
如图,已知抛物线 如图,A是双曲线
如图,A是双曲线