题目内容
已知向量
=（1，2），
•
=10，|
+
|=10，则|
|= ．
| a |
| a |
| b |
| a |
| b |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由模长公式可得|
|，把|
+
|=10平方代入已知数据可得|
|的方程，解方程可得．
| a |
| a |
| b |
| b |
解答：
解：∵
=（1，2），∴|
|=
，
∵
•
=10，|
+
|=10，
∴（
+
）2=
2+2
•
+
2
=5+2×10+|
|2=100，
解得|
|=5
故答案为：5
| a |
| a |
| 5 |
∵
| a |
| b |
| a |
| b |
∴（
| a |
| b |
| a |
| a |
| b |
| b |
=5+2×10+|
| b |
解得|
| b |
| 3 |
故答案为：5
| 3 |
点评：本题考查平面向量数量积的运算，涉及模长公式，属基础题．
练习册系列答案
相关题目
有1=12，1+3=22，1+3+5=32，1+3+5+7=42，…，得到1+3+…+（2n-1）=（ ）
| A、n2 |
| B、n2+1 |
| C、n2-1 |
| D、（n+1）2 |
在△ABC中，A，B，C是三角形的三内角，若sin（A-B）cosB+cos（A-B）sinB≥1，则该三角形是（ ）
| A、等腰三角形 | B、直角三角形 |
| C、正三角形 | D、不存在 |
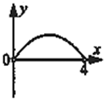
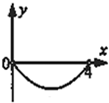
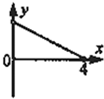
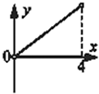
如图，矩形纸片ABCD中，BC=4，AB=3，点P是BC边上的动点，现将△PCD沿PD翻折，得到△PFD；作∠BPF的角平分线交AB于点E．设BP=x，BE=y，则下列图象中，能表示y与x的函数关系的图象大致是（ ）
