题目内容
 如图,矩形纸片ABCD中,BC=4,AB=3,点P是BC边上的动点,现将△PCD沿PD翻折,得到△PFD;作∠BPF的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,矩形纸片ABCD中,BC=4,AB=3,点P是BC边上的动点,现将△PCD沿PD翻折,得到△PFD;作∠BPF的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )A、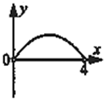 |
B、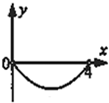 |
C、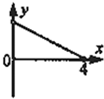 |
D、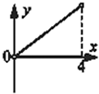 |
考点:函数的图象
专题:函数的性质及应用
分析:根据题意,连接DE,因为△PCD沿PD翻折,得到△PC′D,故有DP平分∠CPC′;又PE为∠BPC′的角平分线,可推知∠EPD=90°,又因为BP=x,BE=y,BC=4,AB=3,分别用x和y表示出PD和EP和DE,在Rt△PED中利用勾股定理,即可得出一个关于x和y的关系式,化简即可.
解答:
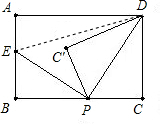 解:连接DE,
解:连接DE,
△PCD沿PD翻折,得到△PC′D,故有DP平分∠CPC′;
又因为PE为∠BPC′的角平分线,
可推知∠EPD=90°,
已知BP=x,BE=y,BC=4,AB=3,
即在Rt△PCD中,PC=4-x,DC=3.即PD2=(4-x)2+9;
在Rt△EBP中,BP=x,BE=y,故PE2=x2+y2;
在Rt△ADE中,AE=3-y,AD=4,故DE2=(3-y)2+16
在Rt△PDE中,DE2=PD2+PE2
即x2+y2+(4-x)2+9=(3-y)2+16
化简得:
y=-
(x2-4x);
结合题意,只有选项D符合题意.
故选A.
 解:连接DE,
解:连接DE,△PCD沿PD翻折,得到△PC′D,故有DP平分∠CPC′;
又因为PE为∠BPC′的角平分线,
可推知∠EPD=90°,
已知BP=x,BE=y,BC=4,AB=3,
即在Rt△PCD中,PC=4-x,DC=3.即PD2=(4-x)2+9;
在Rt△EBP中,BP=x,BE=y,故PE2=x2+y2;
在Rt△ADE中,AE=3-y,AD=4,故DE2=(3-y)2+16
在Rt△PDE中,DE2=PD2+PE2
即x2+y2+(4-x)2+9=(3-y)2+16
化简得:
y=-
| 1 |
| 3 |
结合题意,只有选项D符合题意.
故选A.
点评:本题主要考查了勾股定理的实际应用和对二次函数解析式的分析和读图能力,是一道不错的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
△ABC中,角A,B,C所对的边分别是a,b,c,a=2csinA,则C为( )
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
已知数列:1,a+a2,a2+a3+a4,a3+a4+a5+a6,…,则数列的第k项为( )
| A、ak+ak+1+…+a2k |
| B、ak-1+ak+…+a2k-1 |
| C、ak-1+ak+…+a2k |
| D、ak-1+ak+…+a2k-2 |
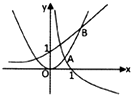 已知y=xa,y=bx,y=logcx中,其中有两个函数具有相反的单调性,另外一个函数是偶函数,如图所示这三个函数部分图象交点A的横坐标是0.65,交点B的横坐标是1.3,则当x∈(0.65,1.3)时,它们的大小关系是( )
已知y=xa,y=bx,y=logcx中,其中有两个函数具有相反的单调性,另外一个函数是偶函数,如图所示这三个函数部分图象交点A的横坐标是0.65,交点B的横坐标是1.3,则当x∈(0.65,1.3)时,它们的大小关系是( )| A、xa>bx>logcx |
| B、bx>logcx>xa |
| C、logcx>xa>bx |
| D、bx>xa>logcx |
已知A、B、C、D为同一球面上的四点,且连接每点间的线段长都等于2,则球心O到平面BCD的距离等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|



