题目内容
已知点(m,n)在曲线
(α为参数)上,点(x,y)在曲线
(β为参数)上,则mx+ny的最大值为( )
|
|
| A、12 | B、15 | C、24 | D、30 |
考点:圆的参数方程
专题:坐标系和参数方程
分析:第一步:将两参数方程化为普通方程,得到m与n,及x与y的关系式;
第二步:将以上得到的两个式子相乘,利用不等式的性质进行放缩,再探求mx+ny的最大值.
第二步:将以上得到的两个式子相乘,利用不等式的性质进行放缩,再探求mx+ny的最大值.
解答:
解:方程
可化为x2+y2=6,由题意得m2+n2=6,
方程
可化为x2+y2=24,
从而(x2+y2)(m2+n2)=(mx)2+(ny)2+(my)2+(nx)2
≥(mx)2+(ny)2+2my•nx=(mx+ny)2,
即6×24≥(mx+ny)2,得mx+ny≤|mx+ny|≤12,
所以mx+ny≤12,
当且仅当my=nx,mx+ny≥0时,mx+ny有最大值12.
故选:A.
|
方程
|
从而(x2+y2)(m2+n2)=(mx)2+(ny)2+(my)2+(nx)2
≥(mx)2+(ny)2+2my•nx=(mx+ny)2,
即6×24≥(mx+ny)2,得mx+ny≤|mx+ny|≤12,
所以mx+ny≤12,
当且仅当my=nx,mx+ny≥0时,mx+ny有最大值12.
故选:A.
点评:1.本题考查了参数方程化普通方程,及不等式性质的运用,属于参数方程与不等式的交汇题.
2.本题容易做错,如mx+ny≤
+
=
=
=15,从而误选B.错误原因在于上式等号不能成立,因为等号成立的条件是:m=x,n=y,联立m2+n2=6及x2+y2=24知,这4个式子不可能同时成立.
2.本题容易做错,如mx+ny≤
| m2+x2 |
| 2 |
| n2+y2 |
| 2 |
| (x2+y2)+(m2+n2) |
| 2 |
| 24+6 |
| 2 |

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
满足sinx≥
的x的集合为( )
| 1 |
| 2 |
A、{x|2kπ+
| ||||
B、{x|2kπ+
| ||||
C、{x|2kπ-
| ||||
D、{x|2kπ-
|
已知函数f(x)=-x2-x+2,则函数y=f(-x)的图象是( )
A、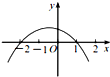 |
B、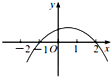 |
C、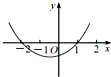 |
D、 |
sin(π+α)=
,则α角的集合是( )
| 1 |
| 2 |
A、{α|α=2kπ+
| ||||
B、{α|α=2kπ-
| ||||
C、{α|α=2kπ+
| ||||
D、{α|α=2kπ-
|
△ABC中,角A,B,C所对的边分别是a,b,c,a=2csinA,则C为( )
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
已知数列:1,a+a2,a2+a3+a4,a3+a4+a5+a6,…,则数列的第k项为( )
| A、ak+ak+1+…+a2k |
| B、ak-1+ak+…+a2k-1 |
| C、ak-1+ak+…+a2k |
| D、ak-1+ak+…+a2k-2 |