题目内容

有1=12，1+3=22，1+3+5=32，1+3+5+7=42，…，得到1+3+…+（2n-1）=（　　）
A、n2
B、n2+1
C、n2-1
D、（n+1）2
考点：归纳推理
专题：推理和证明
分析：可以发现等式左边为连续奇数的和，右边为项数的平方，即可得到答案．
解答： 解：由于1=12，1+3=22，1+3+5=32，1+3+5+7=42，…，
故等式左边为连续奇数的和，右边为项数的平方，
即有1+3+…+（2n-1）=n2．
故选A．
点评：本题主要考查归纳推理及应用，注意观察等式的特点是解题的关键．
练习册系列答案
相关题目
不等式ax2+bx+1＞0的解集为{x|-3＜x＜2}，则a+b=
 
．
已知扇形的圆心角为60°，半径为3cm，则扇形的面积为
 
．
定义在（0，+∞）上的函数f（x）满足：①当x∈[1，3）时，f（x）=1-|x-2|；②f（3x）=3f（x）．设关于x的函数F（x）=f（x）-a的零点从小到大依次为x1，x2，…，xn，…．若a∈（1，3），则x1+x2+…+x2014=
 
．
已知向量
a
=（1，2），
a
•
b
=10，|
a
+
b
|=10，则|
b
|=
 
．
若不等式mx2+mx-4＜2x2+2x-1对任意实数x均成立，则实数m的取值范围是（　　）
A、（-2，2）
B、（-10，2]
C、（-∞，-2）∪[2，+∞）
D、（-∞，-2）
满足sinx≥
1
2
的x的集合为（　　）
A、{x|2kπ+
π
6
≤x≤2kπ+
5π
6
，k∈Z}
B、{x|2kπ+
5π
6
≤x≤2kπ+
7π
6
，k∈Z}
C、{x|2kπ-
π
6
≤x≤2kπ+
π
6
，k∈Z}
D、{x|2kπ-
π
3
≤x≤2kπ+
2π
3
，k∈Z}
sin（π+α）=
1
2
，则α角的集合是（　　）
A、{α|α=2kπ+
7
6
π}
B、{α|α=2kπ-
π
6
}
C、{α|α=2kπ+
π
6
或2kπ+
5
6
π}
D、{α|α=2kπ-
π
6
或2kπ-
5
6
π}
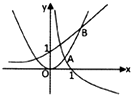已知y=xa，y=bx，y=logcx中，其中有两个函数具有相反的单调性，另外一个函数是偶函数，如图所示这三个函数部分图象交点A的横坐标是0.65，交点B的横坐标是1.3，则当x∈（0.65，1.3）时，它们的大小关系是（　　）
A、xa＞bx＞logcx
B、bx＞logcx＞xa
C、logcx＞xa＞bx
D、bx＞xa＞logcx

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网