题目内容
18.已知tanα,tanβ是方程6x2-5x+1=0两个根且0<α<$\frac{π}{2}$,π<β<$\frac{3π}{2}$,则α+β的值为( )| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{4}$ | D. | $\frac{7π}{4}$ |
分析 先利用韦达定理,求出tanα+tanβ和tanα•tanβ的值,利用正切的两角和公式求出tan(α+β)的值,根据角的范围可求.
解答 解:由题意,tanα+tanβ=$\frac{5}{6}$,tanα•tanβ=-$\frac{1}{6}$,
∴tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=1,
∵0<α<$\frac{π}{2}$,π<β<$\frac{3π}{2}$,可得:α+β∈(π,2π),
∴α+β=$\frac{5π}{4}$
故选:C.
点评 本题的考点是一元二次方程的根的分布与系数的关系,主要考查一元二次方程的根与系数的关系,考查正切的两角和公式及特殊角的三角函数,属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
10.直线l垂直于直线y=x+1,原点O到l的距离为1,且l与y轴正半轴有交点,则直线l的方程是( )
| A. | x+y-$\sqrt{2}$=0 | B. | x+y+1=0 | C. | x+y-1=0 | D. | x+y+$\sqrt{2}$=0 |
7.设a∈R,则1+a+a2+…+an的值为( )
| A. | $\frac{1-{a}^{n}}{1-a}$ | B. | $\frac{1-{a}^{n+1}}{1-a}$ | C. | $\frac{1-{a}^{n+1}}{1-a}$或n+1 | D. | 以上都不是 |
11.执行如图所示的程序框图,如果输入的x,t均为2,则输出的M等于( )
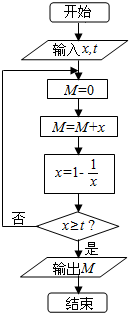

| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |