题目内容
在复平面内，复数z和（2-i）i表示的点关于虚轴对称，则复数z=（ ）
| A、1+2i | B、-1+2i |
| C、-1-2i | D、1-2i |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：直接化简（2-i）i得到点的坐标，然后由复数z和（2-i）i表示的点关于虚轴对称，求出复数z表示的点的坐标，则答案可求．
解答：
解：由（2-i）i=1+2i，
则（2-i）i表示的点的坐标为：（1，2）．
又复数z和（2-i）i表示的点关于虚轴对称，
则复数z表示的点的坐标为：（-1，2）．
∴复数z=-1+2i．
故选：B．
则（2-i）i表示的点的坐标为：（1，2）．
又复数z和（2-i）i表示的点关于虚轴对称，
则复数z表示的点的坐标为：（-1，2）．
∴复数z=-1+2i．
故选：B．
点评：本题考查了复数代数形式的乘法运算，考查了复数的代数表示法及其几何意义，是基础题．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
“m=2”是“直线l1：mx+4y-6=0与直线l2：x+my-3=0平行”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知动点P（a，b）在不等式组
表示的平面区域内部运动，则
的取值范围是（ ）
|
| b+3 |
| a-1 |
A、（-
| ||
| B、（-3，2） | ||
C、（-∞，-
| ||
| D、（1，3） |
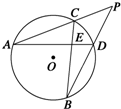如图所示，⊙O的两条弦AD和CB相交于点E，AC和BD的延长线相交于点P，下面结论：①PA•PC=PD•PB；
②PC•CA=PB•BD；
③CE•CD=BE•BA；
④PA•CD=PD•AB．
其中正确的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
把1100（2）化为十进制数，则此数为（ ）
| A、8 | B、12 | C、16 | D、20 |
若（9x-
）n（n∈N*）的展开式的第3项的二项式系数为36，则其展开式中的常数项为（ ）
| 1 | ||
3
|
| A、252 | B、-252 |
| C、84 | D、-84 |
已知定义域为R的奇函数f（x）的导函数为f′（x），当x≠0时，f′（x）+
＞0，若a=
f（
），b=-2f（-2），c=（ln
）f（ln
），则a，b，c的大小关系正确的是（ ）
| f(x) |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a＜c＜b |
| B、b＜c＜a |
| C、a＜b＜c |
| D、c＜a＜b |