题目内容
已知函数y=
+lg(4-x2)的定义域是 (结果用区间表示)
| sin2x |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数成立的条件,即可求出函数的定义域.
解答:
解:要使函数有意义,
则
,
即
,
则-2<x≤-
或0≤x≤
,
故函数的定义域为{x|-2<x≤-
或0≤x≤
},
故答案为:{x|-2<x≤-
或0≤x≤
}.
则
|
即
|
则-2<x≤-
| π |
| 2 |
| π |
| 2 |
故函数的定义域为{x|-2<x≤-
| π |
| 2 |
| π |
| 2 |
故答案为:{x|-2<x≤-
| π |
| 2 |
| π |
| 2 |
点评:本题主要考查函数定义域的求法,要求熟练掌握常见函数成立的条件,比较基础.

练习册系列答案
相关题目
某程序的框图如图所示,执行该程序,若输入的E为0.96,则输出的K为( )


| A、20 | B、22 | C、24 | D、25 |
已知i是虚数单位,复数
=1-bi,其中a、b∈R,则|a+bi|等于( )
| 2-ai |
| i |
| A、-1+2i | ||
| B、1 | ||
C、
| ||
| D、5 |
在复平面内,复数z和(2-i)i表示的点关于虚轴对称,则复数z=( )
| A、1+2i | B、-1+2i |
| C、-1-2i | D、1-2i |

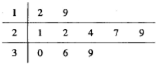 某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )
某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )