题目内容

8．已知某四棱锥的三视图如图所示，俯视图是边长为4的正方形，正视图和侧视图是边长为4的等边三角形，则该四棱锥的全面积为48．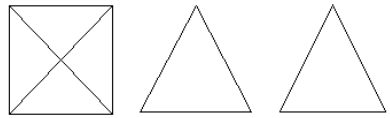

分析 根据几何体的三视图知，该几何体是正四棱锥，
且底面是边长为4的正方形，结合图中数据求出它的全面积．

解答 解：根据几何体的三视图知，
该几何体是正四棱锥，且底面是边长为4的正方形，
正四棱锥的高即等边三角形的高为4×sin$\frac{π}{3}$=2$\sqrt{3}$，
∴斜高为$\sqrt{{（2\sqrt{3}）}^{2}{+2}^{2}}$=4；
∴该四棱锥的全面积为S=42+4×$\frac{1}{2}$×4×4=48．
故答案为：48．

点评 本题考查了利用三视图求几何体全面积的应用问题，是基础题．

练习册系列答案
相关题目
18．已知平面向量$\overrightarrow a，\overrightarrow b$满足$\overrightarrow b•（\overrightarrow a+\overrightarrow b）=3$，且$|\overrightarrow a|=1，|\overrightarrow b|=2$，则向量$\overrightarrow a$与$\overrightarrow b$的夹角（　　）
A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{5π}{6}$
19．已知函数f（x）=x-a-lnx（a∈R）．
（1）若f（x）≥0恒成立，求实数a的取值范围；
（2）证明：若0＜x1＜x2，则x1lnx1-x1lnx2＞x1-x2．
16．在平面直角坐标系xOy中，抛物线y2=2px（p＞0）的焦点为F，准线交x轴于点H，过H作直线l交抛物线于A，B两点，且|BF|=2|AF|．
（Ⅰ）求直线AB的斜率；
（Ⅱ）若△ABF的面积为$\sqrt{2}$，求抛物线的方程．
3．已知某几何体的三视图如图所示，则该几何体的表面积为（　　）
A．16+3πB．12+3πC．8+4$\sqrt{2}$+3πD．4+4$\sqrt{2}$+3π
13．已知命题p：?x∈R，x2-2xsinθ+1≥0；命题q：?α，β∈R，sin（α+β）≤sinα+sinβ，则下列命题中的真命题为（　　）
A．（￢p）∧qB．￢（p∧q）C．（￢p）∨qD．p∧（￢q）
20．设命题p：存在两个相交平面垂直于同一条直线；命题q：?x∈R，x2-2x+1≥0．则下 列命题为真命题的是（　　）
A．p∧qB．p∧（￢q）C．（￢p）∧（￢q）D．（￢p）∧q
17．执行如图所示的程序框图，若x∈[a，b]，y∈[0，4]，则b-a的最小值为（　　）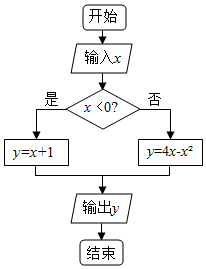
A．2B．3C．4D．5
18．已知i是虚数单位，复数$\frac{1+3i}{1+i}$=（　　）
A．2+iB．2-iC．-1+iD．-1-i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网