题目内容
18.已知i是虚数单位,复数$\frac{1+3i}{1+i}$=( )| A. | 2+i | B. | 2-i | C. | -1+i | D. | -1-i |
分析 利用复数的运算法则即可得出.
解答 解:复数$\frac{1+3i}{1+i}$=$\frac{(1+3i)(1-i)}{(1+i)(1-i)}$=$\frac{4+2i}{2}$=2+i,
故选:A.
点评 本题考查了复数的运算法则,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
9.设a、b、c是正实数,则“a、b、c依次成等差数列”是“$b≥\sqrt{ac}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
3.已知角α的终边与单位圆交于点(-$\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$),则sin2α的值为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | -$\frac{\sqrt{5}}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
10.求函数f(x)=x+$\frac{1}{x}$-1-ln(x+3)零点的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的渐近线与抛物线x2=4y的准线所围成的三角形面积为2,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
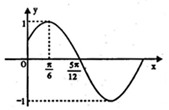 已知函数f(x)=Msin(ωx+φ)(M>0)的部分图象如图所示.
已知函数f(x)=Msin(ωx+φ)(M>0)的部分图象如图所示. 图形的对称,正弦曲线的流畅都能体现“数学美”.“黄金分割”也是数学美得 一种体现,如图,椭圆的中心在原点,F为左焦点,当$\overrightarrow{FB}⊥\overrightarrow{AB}$时,其离心率为$\frac{{\sqrt{5}-1}}{2}$,此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于$\frac{\sqrt{5}+1}{2}$.
图形的对称,正弦曲线的流畅都能体现“数学美”.“黄金分割”也是数学美得 一种体现,如图,椭圆的中心在原点,F为左焦点,当$\overrightarrow{FB}⊥\overrightarrow{AB}$时,其离心率为$\frac{{\sqrt{5}-1}}{2}$,此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于$\frac{\sqrt{5}+1}{2}$.