题目内容
已知cos（α+
）-sinα=
，则cos（
+α）的值为 ．
| π |
| 6 |
| ||
| 6 |
| π |
| 3 |
考点：两角和与差的余弦函数
专题：三角函数的求值
分析：利用两角和的余弦将cos（α+
）展开，再利用辅助角公式化简整理，即可求得cos（
+α）的值．
| π |
| 6 |
| π |
| 3 |
解答：
解：∵cos（α+
）-sinα=cosαcos
-sinαsin
-sinα=
cosα-
sinα=
cos（α+
）=
，
∴cos（
+α）=
．
故答案为：
．
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
| ||
| 6 |
∴cos（
| π |
| 3 |
| 1 |
| 6 |
故答案为：
| 1 |
| 6 |
点评：本题考查两角和与差的余弦，考查三角恒等变换的应用，属于中档题．
练习册系列答案
相关题目
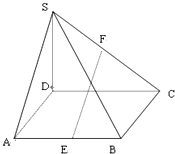如图所示，在四棱锥S-ABCD中，SD⊥底面ABCD，四边形ABCD为矩形，E、F分别为AB、SC的中点，且AD=SD=2，DC=3．若a=9，b=12，A=45°，则△ABC有（ ）
| A、一解 | B、两解 |
| C、无解 | D、不能确定 |
