题目内容

若a=9，b=12，A=45°，则△ABC有（　　）
A、一解B、两解
C、无解D、不能确定
考点：解三角形
专题：计算题,解三角形
分析：根据余弦定理，建立a2关于b、c和cosA的式子，得到关于边c的一元二次方程，解之得c=6
2
±3．由此可得此三角形有两解，得到本题的答案．
解答： 解答：∵△ABC中，a=9，b=12，A=45°，
∴由余弦定理a2=b2+c2-2bccosA，得92=122+c2-2×12ccos45°，
化简整理，得c2-12
2
c+63=0，解之得c=6
2
±3
因此，△ABC的三条边分别为：a=9、b=12、c=6
2
-3，或a=9、b=12、c=6
2
+3
可得此三角形解的个数有2个
故选：B．
点评：本题给出三角形两边及一边对夹角的大小，求三角形的解的个数，着重考查了利用正弦定理和余弦定理解三角形的知识，属于基本知识的考查．
练习册系列答案
相关题目
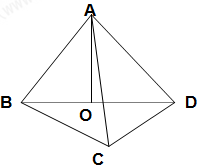设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O，AC=BC=1，CD=
2
．
（1）AC与平面BCD所成角的大小；
（2）二面角A-BC-D的正切值．
已知tan（θ+
π
4
）=3，则sin2θ-2cos2θ=
 
．
某市2010年底有住房面积1200万平方米，计划从2011年起，每年拆除20万平方米的旧住房，假定该市每年新建保障性等住房面积是上年年底住房面积的5%．
（1）请求出2012年底的住房面积．
（2）到哪年年底，该市的住房面积开始超过2520万平方米？
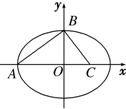如图，A、B、C分别为椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的顶点与焦点，若∠ABC=90°，
求该椭圆的离心率．
已知cos（α+
π
6
）-sinα=
3
6
，则cos（
π
3
+α）的值为
 
．
对于定义域为[0，1]的函数f（x），如果同时满足以下三个条件：
①对任意的x∈[0，1]，总有f（x）≥0
②f（1）=1
③若x1≥0，x2≥0，x1+x2≤1，都有f（x1+x2）≥f（x1）+f（x2） 成立；则称函数f（x）为理想函数．试证明下列三个命题：
（1）若函数f（x）为理想函数，则f（0）=0；
（2）函数f（x）=2x-1（x∈[0，1]）是理想函数；
（3）若函数f（x）是理想函数，假定存在x0∈[0，1]，使得f（x0）∈[0，1]，且f[f（x0）]=x0，则f（x0）=x0．
△ABC是等腰直角三角形，已知A（1，1），B（1，3），AB⊥BC，点C在第一象限，点（x，y）在△ABC内部，则点C的坐标为
 
，z=2x-y的最大值是
 
．
等比数列{an}共有20项，其中前四项的积是
1
128
，末四项的积是512，则这个等比数列的各项乘积是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网