题目内容
曲线y=x2与y=x所围成图形的面积是 .
考点:定积分在求面积中的应用
专题:计算题,导数的概念及应用
分析:先根据题意画出区域,然后依据图形得到积分下限为0,积分上限为1,从而利用定积分表示出曲边梯形的面积,最后用定积分的定义求出所求即可.
解答:
 解:先根据题意画出图形,得到积分上限为1,积分下限为0
解:先根据题意画出图形,得到积分上限为1,积分下限为0
直线y=x与曲线y=x2所围图形的面积S=∫01(x-x2)dx
而∫01(x-x2)dx=(
x2-
x3)|01=
-
=
∴曲边梯形的面积是
.
故答案为:
.
 解:先根据题意画出图形,得到积分上限为1,积分下限为0
解:先根据题意画出图形,得到积分上限为1,积分下限为0直线y=x与曲线y=x2所围图形的面积S=∫01(x-x2)dx
而∫01(x-x2)dx=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
∴曲边梯形的面积是
| 1 |
| 6 |
故答案为:
| 1 |
| 6 |
点评:本题主要考查了学生会求出原函数的能力,以及考查了数形结合的思想,同时会利用定积分求图形面积的能力,解题的关键就是求原函数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设点P在曲线ρsinθ=2上,点Q在曲线ρ=-2cosθ上,则|PQ|的最小值为( )
| A、2 | B、1 | C、3 | D、0 |
若a>b,则下列各项正确的是( )
| A、ac>bc |
| B、ax2>bx2 |
| C、a2>b2 |
| D、a2x>b2x |
 如图,在圆O中,O为圆心,AB为圆的一条弦,AB=6,则
如图,在圆O中,O为圆心,AB为圆的一条弦,AB=6,则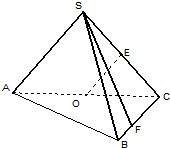 如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC,AC的中点,SA=SC=
如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC,AC的中点,SA=SC=