题目内容
16.复数${({1+i})^2}+\frac{2}{1+i}$的共轭复数的虚部是( )| A. | i | B. | -i | C. | -1 | D. | 1 |
分析 利用复数的运算法则、虚部的定义即可得出.
解答 解:${({1+i})^2}+\frac{2}{1+i}$=2i+$\frac{2(1-i)}{(1+i)(1-i)}$=2i+1-i=1+i的共轭复数1-i的虚部是-1.
故选:C.
点评 本题考查了复数的运算法则,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
1.如果实数x,y满足关系$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-2≤0}\\{y≥0}\end{array}\right.$,又$\frac{2x+y-7}{x-3}$≥c恒成立,则c的取值范围为( )
| A. | (-∞,$\frac{9}{5}$] | B. | (-∞,3] | C. | [$\frac{9}{5}$,+∞) | D. | [3,+∞) |
5.在区域$Ω=\left\{{(x,y)|\left\{\begin{array}{l}x≥0\\ x+y≤1\\ x-y≤1\end{array}\right.}\right\}$中,若满足ax+y>0的区域面积占Ω面积的$\frac{1}{3}$,则实数a的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{2}{3}$ |




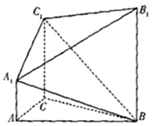 如图,在几何体A1B1C1-ABC中,∠ACB=90°,AC=BC=2,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1,且AA1=1.
如图,在几何体A1B1C1-ABC中,∠ACB=90°,AC=BC=2,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1,且AA1=1.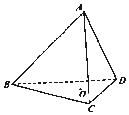 如图,在正四面体ABCD中,O是△BCD的中心,E,F分别是AB,AC上的动点,且$\overrightarrow{BE}$=λ$\overrightarrow{BA}$,$\overrightarrow{CF}$=(1-λ)$\overrightarrow{CA}$
如图,在正四面体ABCD中,O是△BCD的中心,E,F分别是AB,AC上的动点,且$\overrightarrow{BE}$=λ$\overrightarrow{BA}$,$\overrightarrow{CF}$=(1-λ)$\overrightarrow{CA}$