题目内容
1.如果实数x,y满足关系$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-2≤0}\\{y≥0}\end{array}\right.$,又$\frac{2x+y-7}{x-3}$≥c恒成立,则c的取值范围为( )| A. | (-∞,$\frac{9}{5}$] | B. | (-∞,3] | C. | [$\frac{9}{5}$,+∞) | D. | [3,+∞) |
分析 作出不等式组对应的平面区域,利用目标函数分式的几何意义求出其最小值,即可求出c的取值范围.
解答 解:设z=$\frac{2x+y-7}{x-3}$=2+$\frac{y-1}{x-3}$
z的几何意义是区域内的点到D(3,1)的斜率加2,
作出不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-2≤0}\\{y≥0}\end{array}\right.$对应的平面区域如图:
由图形,可得C($\frac{1}{2}$,$\frac{3}{2}$),
由图象可知,直线CD的斜率最小值为$\frac{2×\frac{1}{2}+\frac{3}{2}-7}{\frac{1}{2}-3}$=$\frac{9}{5}$,
∴z的最小值为$\frac{9}{5}$,
∴c的取值范围是(-∞,$\frac{9}{5}$].
故选:A.
点评 本题主要考查了线性规划的应用问题,利用直线斜率的几何意义求最小值是解题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
11.若将函数f(x)=$\left\{\begin{array}{l}{2|x|-2,x∈[-1,1]}\\{f(x-2),x∈(1,+∞)}\end{array}\right.$的正零点从小到大依次排成一列,得到数列{an},n∈N*,则数列{(-1)n+1an}的前2017项和为( )
| A. | 4032 | B. | 2016 | C. | 4034 | D. | 2017 |
16.复数${({1+i})^2}+\frac{2}{1+i}$的共轭复数的虚部是( )
| A. | i | B. | -i | C. | -1 | D. | 1 |
13.已知集合A={x|0<x<2},集合B={x|-1<x<1},集合C={x|mx+1>0},若A∪B⊆C,则实数m的取值范围为( )
| A. | {m|-2≤m≤1} | B. | {m|-$\frac{1}{2}$≤m≤1} | C. | {m|-1≤m≤$\frac{1}{2}$} | D. | {m|-$\frac{1}{2}$≤m≤$\frac{1}{4}$} |
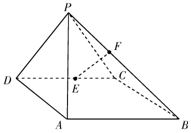 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,$AB=DP=2\sqrt{2}$,E为CD的中点,点F在线段PB上.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,$AB=DP=2\sqrt{2}$,E为CD的中点,点F在线段PB上.