题目内容
已知数列{an}满足:a1=1,2an+1=2an+1,n∈N+.数列{bn}的前n项和为Sn,Sn=9-(
)n-2,n∈N+.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=an•bn,n∈N+.求数列{cn}的前n项和Tn.
| 1 |
| 3 |
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=an•bn,n∈N+.求数列{cn}的前n项和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)根据数列的递推关系即可求数列{an},{bn}的通项公式;
(Ⅱ)求出数列{cn}的通项公式,利用错位相减法即可求出数列{cn}的前n项和Tn.
(Ⅱ)求出数列{cn}的通项公式,利用错位相减法即可求出数列{cn}的前n项和Tn.
解答:
解:(Ⅰ)由2an+1=2an+1得an+1-an=
,
又a1=1,所以数列{an}是以1为首项,
为公差的等差数列,
于是an=a1+(n-1)d=
,
当n=1时,b1=S1=9-(
)1-2=9-3=6,
当n≥2时,Sn-1=9-(
)n-3,
则bn=Sn-Sn-1=9-(
)n-2-[9-(
)n-3]=
,
又n=1时,
=6=b1,
所以bn=
.
(Ⅱ)由(Ⅰ)知an=
,bn=
,
所以cn=an•bn=(n+1)(
)n-2,
所以Tn=2×(
)-1+3×(
)0+4×(
)1+…+(n+1)×(
)n-2 …(1)
等式两边同乘以
得
Tn=2×(
)0+3×(
)1+4×(
)2+…+(n+1)×(
)n-1…(2)
(1)-(2)得
Tn=2×(
)-1+(
)0+(
)1+…+×(
)n-2-(n+1)×(
)n-1=6+
-(n+1)×(
)n-1,
所以Tn=
-
•(
)n-2.
| 1 |
| 2 |
又a1=1,所以数列{an}是以1为首项,
| 1 |
| 2 |
于是an=a1+(n-1)d=
| n+1 |
| 2 |
当n=1时,b1=S1=9-(
| 1 |
| 3 |
当n≥2时,Sn-1=9-(
| 1 |
| 3 |
则bn=Sn-Sn-1=9-(
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3n-2 |
又n=1时,
| 2 |
| 3n-2 |
所以bn=
| 2 |
| 3n-2 |
(Ⅱ)由(Ⅰ)知an=
| n+1 |
| 2 |
| 2 |
| 3n-2 |
所以cn=an•bn=(n+1)(
| 1 |
| 3 |
所以Tn=2×(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
等式两边同乘以
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(1)-(2)得
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
1-(
| ||
1-
|
| 1 |
| 3 |
所以Tn=
| 45 |
| 4 |
| 2n+5 |
| 4 |
| 1 |
| 3 |
点评:本题主要考查数列的通项公式以及数列的求和,利用错位相减法是解决本题的关键.

练习册系列答案
相关题目
动点P到点A(8,0)的距离是到点B(2,0)的距离的2倍,则动点P的轨迹方程为( )
| A、x2+y2=32 |
| B、x2+y2=16 |
| C、(x-1)2+y2=16 |
| D、x2+(y-1)2=16 |
已知实数x、y满足不等式组
,则3x+y的取值范围为( )
|
A、[-3,-
| ||||
B、[-3,-
| ||||
C、[-
| ||||
D、[-
|
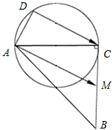 如图,已知:|AC|=|BC|=2,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则
如图,已知:|AC|=|BC|=2,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则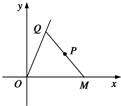 有定点P(6,4)及定直线l:y=4x,点Q是l上在第一象限内的点,PQ交x轴的正半轴于点M,
有定点P(6,4)及定直线l:y=4x,点Q是l上在第一象限内的点,PQ交x轴的正半轴于点M,