题目内容
已知-1，a，b，c，-4成等比数列，则实数b为（ ）
| A、4 | B、-2 | C、±2 | D、2 |
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：利用等比数列的性质求得b=±2，验证b=2不合题意，从而求得b=-2．
解答：
解：∵-1，a，b，c，-4成等比数列，
∴b2=（-1）×（-4）=4，
则b=±2，
当b=2时，a2=（-1）×2=-2，不合题意，舍去．
∴b=-2．
故选：B．
∴b2=（-1）×（-4）=4，
则b=±2，
当b=2时，a2=（-1）×2=-2，不合题意，舍去．
∴b=-2．
故选：B．
点评：本题考查了等比数列的通项公式，考查了等比数列的性质，是基础的计算题．
练习册系列答案
考前必练系列答案
相关题目
执行如图所示的程序框图，则输出的b值等于（ ）| A、-3 | B、-8 |
| C、-15 | D、-24 |
执行如图所示的程序框图，输出i的值为（ ）
| A、2 | B、3 | C、4 | D、5 |
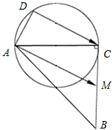如图，已知：|AC|=|BC|=2，∠ACB=90°，M为BC的中点，D为以AC为直径的圆上一动点，则
