题目内容
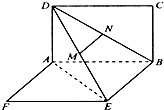 如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1,线段AB的长为
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1,线段AB的长为考点:与二面角有关的立体几何综合题
专题:空间位置关系与距离
分析:利用已知可知∠DEA为DE与平面ABEF所成的角,从而∠DEA=45°.在Rt△DAE中,∠DAE=90°,AE=DE•cos∠DEA=2.从而得到在Rt△ABE中,AB=2.
解答:
解:∵平面ABCD⊥平面ABEF,且平面ABCD∩平面ABEF=AB,EB⊥AB,
∴EB⊥平面ABCD,又MN∥EB,
∴MN⊥面ABCD.
∴∠EDB为DE与平面ABCD所成的角,∴∠EDB=30°.
又在Rt△EBD中,EB=2MN=2,∠EBD=90°∴DE=4,
连接AE,可知∠DEA为DE与平面ABEF所成的角,∴∠DEA=45°.
在Rt△DAE中,∠DAE=90°,∴AE=DE•cos∠DEA=2.
在Rt△ABE中,AB=2.
故答案为:2.
∴EB⊥平面ABCD,又MN∥EB,
∴MN⊥面ABCD.
∴∠EDB为DE与平面ABCD所成的角,∴∠EDB=30°.
又在Rt△EBD中,EB=2MN=2,∠EBD=90°∴DE=4,
连接AE,可知∠DEA为DE与平面ABEF所成的角,∴∠DEA=45°.
在Rt△DAE中,∠DAE=90°,∴AE=DE•cos∠DEA=2.
在Rt△ABE中,AB=2.
故答案为:2.
点评:本题考查线段长的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
设α是第二象限角,P(x,4)为其终边上的一点,且cosα=
x,则tanα等于( )
| 1 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知实数x、y满足不等式组
,则3x+y的取值范围为( )
|
A、[-3,-
| ||||
B、[-3,-
| ||||
C、[-
| ||||
D、[-
|
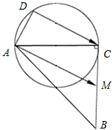 如图,已知:|AC|=|BC|=2,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则
如图,已知:|AC|=|BC|=2,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则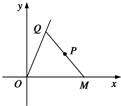 有定点P(6,4)及定直线l:y=4x,点Q是l上在第一象限内的点,PQ交x轴的正半轴于点M,
有定点P(6,4)及定直线l:y=4x,点Q是l上在第一象限内的点,PQ交x轴的正半轴于点M,
