题目内容
一个箱子装有8个白球和7个黑球,一次摸出4个球,求:
①摸到的都是白球的概率;
②在已知它们颜色相同的情况下,该颜色是白球的概率.
①摸到的都是白球的概率;
②在已知它们颜色相同的情况下,该颜色是白球的概率.
考点:条件概率与独立事件
专题:概率与统计
分析:①根据题意,首先计算取出四个球都是白球的情况数目,再求取四个球情况数目,进而由等可能事件的概率公式,计算可得答案,
②再计算取出四球都是黑球的情况数目,两者相加可得取出四球颜色相同的情况数目,进而由等可能事件的概率公式,计算可得答案.
②再计算取出四球都是黑球的情况数目,两者相加可得取出四球颜色相同的情况数目,进而由等可能事件的概率公式,计算可得答案.
解答:
解:①8个白球中取4个白球有C84=70种,15个球中取4个球有C154=1365种,
故一次摸出4个球,摸到的都是白球的概率为
=
,
②8个白球中取4个白球有C84=70种,
7个黑球中取4个黑球有C74=35种,
则一次摸出4个球,它们的颜色相同的有70+35=105种;
故一次摸出4个球,在已知它们的颜色相同的情况下,该颜色是白色的概率为
=
故一次摸出4个球,摸到的都是白球的概率为
| 70 |
| 1365 |
| 2 |
| 39 |
②8个白球中取4个白球有C84=70种,
7个黑球中取4个黑球有C74=35种,
则一次摸出4个球,它们的颜色相同的有70+35=105种;
故一次摸出4个球,在已知它们的颜色相同的情况下,该颜色是白色的概率为
| 70 |
| 105 |
| 2 |
| 3 |
点评:本题主要考查了等可能事件的概率,关键是对条件“在已知它们的颜色相同的情况下”的理解,也可以由条件概率来求解

练习册系列答案
相关题目
已知函数f(x)=|x-1|,x∈R.设a=f[f(
)],b=f[f(-
)],则( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、a>b | B、a<b |
| C、a=b | D、a≠b |
已知α∈(
,π),且sinα=
,则tanα=( )
| π |
| 2 |
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
设M是△ABC所在平面上的一点,且
+
+
=
,D是AC中点,则
的值为( )
| MB |
| 3 |
| 2 |
| MA |
| 3 |
| 2 |
| MC |
| 0 |
|
| ||
| |BM| |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
动点P到点A(8,0)的距离是到点B(2,0)的距离的2倍,则动点P的轨迹方程为( )
| A、x2+y2=32 |
| B、x2+y2=16 |
| C、(x-1)2+y2=16 |
| D、x2+(y-1)2=16 |
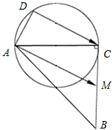 如图,已知:|AC|=|BC|=2,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则
如图,已知:|AC|=|BC|=2,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则