题目内容
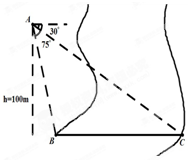 如图,在气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,若此时的气球高度是100m,则河流在B,C两地的宽度为
如图,在气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,若此时的气球高度是100m,则河流在B,C两地的宽度为考点:正弦定理,余弦定理
专题:计算题,解三角形
分析:设直线AB与过A点垂直于AB的直线交于点D,分别在Rt△ACD、Rt△ABD中利用三角函数的定义,算出CD、BD的长,从而可得BC=200(
-1)m,即为河流在B、C两地的宽度.
| 3 |
解答:
解: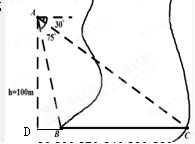 设直线AB与过A点垂直于AB的直线交于点D,
设直线AB与过A点垂直于AB的直线交于点D,
则Rt△ACD中,∠C=30°,AD=100m
∴CD=
=100
m.
又∵Rt△ABD中,∠ABD=75°,可得BD=
=100(2-
)m
∴AB=AD-BD=200(
-1)m
故答案为:200(
-1)m
 设直线AB与过A点垂直于AB的直线交于点D,
设直线AB与过A点垂直于AB的直线交于点D,则Rt△ACD中,∠C=30°,AD=100m
∴CD=
| AD |
| tan30° |
| 3 |
又∵Rt△ABD中,∠ABD=75°,可得BD=
| AD |
| tan75° |
| 3 |
∴AB=AD-BD=200(
| 3 |
故答案为:200(
| 3 |
点评:本题给出实际应用问题,求河流在B、C两地的宽度,着重考查了三角函数的定义、正余弦定理解三角形的知识,属于中档题.

练习册系列答案
相关题目
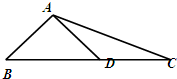 如图,在△ABC中,AD⊥AB,
如图,在△ABC中,AD⊥AB,