题目内容
16.已知f(x)=$\left\{\begin{array}{l}{lo{g}_{a}x,x>1}\\{(6-a)^{x}-2a,x≤1}\end{array}\right.$.(1)若a=4,求f(f(2))的值;
(2)若f(x)是R上的单调递增函数,求实数a的取值范围.
分析 (1)由内而外求f(f(2))的值,即先求得f(2),再将之代入函数式求值;
(2)f(x)为增函数需要满足三条件,对数函数递增,指数函数递增,在分界点附近递增,列出不等式得出a的取值范围.
解答 解:(1)当a=4时,f(2)=log42=$\frac{1}{2}$,
而f($\frac{1}{2}$)=$(6-4)^{\frac{1}{2}}-8$=$\sqrt{2}$-8,
即f(f(2))=$\sqrt{2}$-8;
(2)∵f(x)是R上的单调递增函数,
∴a>1且6-a>1,
解得,1<a<5,-----------------①
当x=1时,loga1=0>(6-a)-2a,
解得,a≥2,--------------------②
由①②得,2≤a<5,
所以实数a的取值范围为:[2,5).
点评 本题主要考查了分段函数的图象与性质,涉及分段函数值的求解和分段函数单调性的确定,属于中档题.

练习册系列答案
相关题目
6.直线x+y=5与直线x-y=1交点坐标是( )
| A. | (1,2) | B. | (2,3) | C. | (3,2) | D. | (2,1) |
1.在复平面内,复数$\frac{2}{1-i}$+2i2对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
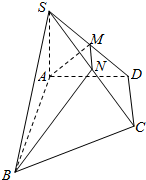 如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,CD=DA=a,AB=2a,SA⊥平面ABCD,且SA=a
如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,CD=DA=a,AB=2a,SA⊥平面ABCD,且SA=a