题目内容
5.已知f(x)是定义在R上的奇函数,当X≥0时,f(x)=2x-1.(1)求当x<0时,f(x)的解析式;
(2)若f(x)≤5,求x的取值范围.
分析 (1)当x<0时,-x>0,结合题意以及函数的奇偶性可得;
(2)f(x)≤5等价于$\left\{\begin{array}{l}{x<0}\\{2x+1≤5}\end{array}\right.$或$\left\{\begin{array}{l}{x≥0}\\{2x-1≤5}\end{array}\right.$,分别解不等式组综合可得.
解答 解:(1)当x<0时,-x>0,
∵当x≥0时,f(x)=2x-1,
∴f(-x)=-2x-1,
又∵f(x)是定义在R上的奇函数,
∴-f(x)=f(-x)=-2x-1,
∴当x<0时,f(x)的解析式为f(x)=2x+1;
(2)由(1)可知f(x)=$\left\{\begin{array}{l}{2x+1,x<0}\\{2x-1,x≥0}\end{array}\right.$,
∴f(x)≤5等价于$\left\{\begin{array}{l}{x<0}\\{2x+1≤5}\end{array}\right.$或$\left\{\begin{array}{l}{x≥0}\\{2x-1≤5}\end{array}\right.$,
分别解不等式组可得x<0或0≤x≤3,
∴x的取值范围为(-∞,3]
点评 本题考查函数解析式的求解方法,涉及函数的奇偶性和不等式组的解法,属基础题.

练习册系列答案
相关题目
20.执行下列程序框图,则输出结果为( )


| A. | 413 | B. | 404 | C. | 397 | D. | 407 |
17.如图程序框图表示的算法是:求1+2+3+4+…+n>20时n的最小值,则输出框中应填( )


| A. | i | B. | i+1 | C. | i-1 | D. | n |
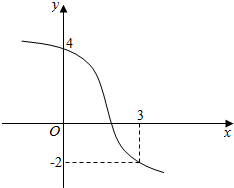 已知函数f(x)的部分图象如图所示,若不等式-2<f(x+t)<4的解集为(-1,2),则实数t的值为-1.(写过程)
已知函数f(x)的部分图象如图所示,若不等式-2<f(x+t)<4的解集为(-1,2),则实数t的值为-1.(写过程)