题目内容

1．在复平面内，复数$\frac{2}{1-i}$+2i2对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

分析 利用复数的运算法则、几何意义即可得出．

解答 解：在复平面内，复数$\frac{2}{1-i}$+2i2=$\frac{2（1+i）}{（1-i）（1+i）}$-2=1+i-2=-1+i的点（-1，1）位于第二象限．
故选：B．

点评 本题考查了复数的运算法则、几何意义，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
11．如果两个球的体积之比为8：27，那么两个球的半径之比为（　　）
A．8：27B．2：3C．4：9D．2：9
12．如图所示的程序框图，输出的结果是15．
9．已知函数f（x）（x∈D），若存在常数T（T＞0），对任意x∈D都有f（x+T）=T•f（x），则称函数f（x）为T倍周期函数
（1）判断h（x）=x是否是T倍周期函数，并说明理由．
（2）证明$g（x）={（{\frac{1}{4}}）^x}$是T倍周期函数，且T的值是唯一的．
（3）若f（n）（n∈N*）是2倍周期函数，f（1）=1，f（2）=-4，Sn表示f（n）的前n 项和，Cn=$\frac{{{S_{2n}}}}{{{S_{2n-1}}}}$，若Cn＜loga（a+1）+10恒成立，求a的取值范围．
16．已知f（x）=$\left\{\begin{array}{l}{lo{g}_{a}x，x＞1}\\{（6-a）^{x}-2a，x≤1}\end{array}\right.$．
（1）若a=4，求f（f（2））的值；
（2）若f（x）是R上的单调递增函数，求实数a的取值范围．
6．已知函数f（x）=x3+x2-$\frac{1}{27}$，则关于x的方程3（f（x））2+2f（x）=0的根的个数为（　　）
A．2B．3C．4D．5
13．已知数列{an}的前n项和Sn满足：Sn=an2+bn，且a1=1，a2=3．
（I）求数列{an}的通项公式；
（Ⅱ）记bn=2${\;}^{{a}_{n}}$，数列{bn}的前n项和Tn，求证：Tn≥2．
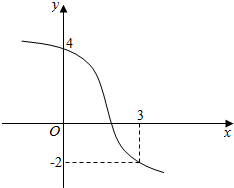10．已知函数f（x）的部分图象如图所示，若不等式-2＜f（x+t）＜4的解集为（-1，2），则实数t的值为-1．（写过程）
11．已知向量$\overrightarrow{m}$=（$\sqrt{3}$，1），向量$\overrightarrow{n}$是与$\overrightarrow{m}$垂直的单位向量．若向量$\overrightarrow{n}$与向量（1.2）的夹角b锐角，且与向量$\overrightarrow{p}$=（x-y2，$\sqrt{3}$x）垂直，则t=y2+5x2+4的最小值为4．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网