题目内容
某园艺师培育了两种珍稀树苗A与B,株数分别为12与18,现将这30株树苗的高度编写成如茎叶图(单位:cm):

在这30株树苗中,树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.
(1)对于这30株树苗,如果用分层抽样的方法从“生长良好”和“非生长良好”中共抽取5株,再从这5株中任选2株,那么至少有一株“生长良好”的概率是多少?
(2)若从所有“生长良好”中选3株,用X表示所选中的树苗中能出售的株树,试写出X的分布列,并求X的数学期望.

在这30株树苗中,树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.
(1)对于这30株树苗,如果用分层抽样的方法从“生长良好”和“非生长良好”中共抽取5株,再从这5株中任选2株,那么至少有一株“生长良好”的概率是多少?
(2)若从所有“生长良好”中选3株,用X表示所选中的树苗中能出售的株树,试写出X的分布列,并求X的数学期望.
考点:离散型随机变量的期望与方差,茎叶图,古典概型及其概率计算公式
专题:综合题,概率与统计
分析:(1)根据茎叶图,可知“生长良好”有12株,“非生长良好”的有18株,用分层抽样的方法,求出“生长良好”和“非生长良好”的株数,利用对立事件的概率,即可求出至少有一株“生长良好”的概率;
(2)由题设知X的可能取值分别为0,1,2,3,分别求出P(X=0),P(X=1),P(X=2),P(X=3),由此能求出X的分布列和EX.
(2)由题设知X的可能取值分别为0,1,2,3,分别求出P(X=0),P(X=1),P(X=2),P(X=3),由此能求出X的分布列和EX.
解答:
解:(1)根据茎叶图,可知“生长良好”有12株,“非生长良好”的有18株,
用分层抽样的方法从“生长良好”和“非生长良好”中共抽取5株,“生长良好”的有2株,“非生长良好”的有3株.
∴至少有一株“生长良好”的概率是1-
=
;
(2)从所有“生长良好”中选3株,其中A种树苗有8株,B种树苗有4株,则X的可能取值分别为0,1,2,3,
P(X=0)=
=
;P(X=1)=
=
;P(X=2)=
=
;P(X=3)=
=
,
∴X的分布列为:
∴EX=0×
+1×
+2×
+3×
=1.
用分层抽样的方法从“生长良好”和“非生长良好”中共抽取5株,“生长良好”的有2株,“非生长良好”的有3株.
∴至少有一株“生长良好”的概率是1-
| ||
|
| 7 |
| 10 |
(2)从所有“生长良好”中选3株,其中A种树苗有8株,B种树苗有4株,则X的可能取值分别为0,1,2,3,
P(X=0)=
| ||
|
| 14 |
| 55 |
| ||||
|
| 28 |
| 55 |
| ||||
|
| 12 |
| 55 |
| ||
|
| 1 |
| 55 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 14 |
| 55 |
| 28 |
| 55 |
| 12 |
| 55 |
| 1 |
| 55 |
点评:本题考查离散型随机变量的分布列和数学期望,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
已知等差数列{an}中,a7=
,则a6+a7+a8等于( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
| D、111 |
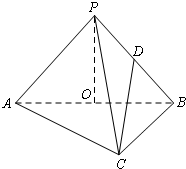 如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,连结CD.
如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,连结CD. 经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出15条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如图.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm.
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出15条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如图.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm.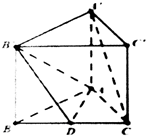 如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2
如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2