题目内容
设u=(x,y)=|ex-y|-y|x-lny|,x,y∈R.
(1)若a>0,令f(x)=(x,a),判断f(x)的单调性;
(2)若0<a<b,令F(x)=u(x,a)-u(x,b),试求函数F(x)的最小值;
(3)记(2)中的最小值为T(a,b),证明:T(a,b)>0.
(1)若a>0,令f(x)=(x,a),判断f(x)的单调性;
(2)若0<a<b,令F(x)=u(x,a)-u(x,b),试求函数F(x)的最小值;
(3)记(2)中的最小值为T(a,b),证明:T(a,b)>0.
考点:利用导数研究函数的单调性,导数在最大值、最小值问题中的应用
专题:证明题,综合题,导数的综合应用
分析:(1)通过对x分x≥lna与x≤lna的讨论,去掉绝对值符号,再利用导数判断函数的单调性;
(2)通过对x分①x≤lna<lnb,②lna≤x≤lnb,③lna<lnb≤x三类讨论,利用导数可判断各区间上的单调性及最值情况,从而可求得F(x)有最小值;
(3)将所证的不等式进行等价变形,构造函数g(x)=xlnx,利用两次求导说明函数的凸凹性,从而得证.
(2)通过对x分①x≤lna<lnb,②lna≤x≤lnb,③lna<lnb≤x三类讨论,利用导数可判断各区间上的单调性及最值情况,从而可求得F(x)有最小值;
(3)将所证的不等式进行等价变形,构造函数g(x)=xlnx,利用两次求导说明函数的凸凹性,从而得证.
解答:
解:(1)f(x)=|ex-a|-a|x-ln a|(a>0),
函数f(x)的定义域为R,
当x≥lna时,ex≥a,f(x)=ex-ax+alna-a,
∵f′(x)=ex-a≥0,
∴f(x)在[lna,+∞)上为增函数,
当x≤lna时,ex≤a,f(x)=ax-ex-alna+a,
∵f′(x)=a-ex≥0,
∴f(x)在(-∞,lna]上为增函数,
综上所述,f(x)在定义域R内为增函数;
(2)易知F(x)的定义域为R,F′(x)=u′(x,a)-u′(x,b),而0<a<b,
∴lna<lnb,由(1)容易得到下列结论:
①当x≤lna<lnb时,F′(x)=(a-ex)-(b-ex)=a-b<0,
∴F(x)在(-∞,lna]上为减函数,从而F(x)≥F(lna),
②lna≤x≤lnb时,F′(x)=(ex-a)-(b-ex)=2ex-(a+b),
令F′(x)=0,得x=ln
,
当lna≤x<ln
时,时,F′(x)<0,F,(x)单调递减,
当ln
<x≤lnb时,F′(x)>0,F,(x)单调递增,
∴当x=ln
时,F(x)有最小值F(ln
),
③lna<lnb≤x时,F′(x)=(ex-a)-(ex-b)=b-a>0,
∴F(x)在[lnb,+∞)上为增函数,从而F(x)≥F(lnb)
综上所述,当x=ln
时,
F(x)有最小值F(ln
)=alna+blnb-(a+b)ln
;
(3)由(2)知T(a,b)=alna+blnb-(a+b)ln
,
要证T(a,b)>0,即证alna+blnb>(a+b)ln
,
等价为证:
>
ln
,
设g(x)=xlnx,则
上式等价为
>f(
),
即证明函数g(x)为凹函数即可.
∵g'(x)=1+lnx,g''(x)=
>0恒成立,
∴函数g(x)为凹函数,
即
>f(
)成立.
∴alna+blnb>(a+b)ln
成立.
∴T(a,b)>0.
函数f(x)的定义域为R,
当x≥lna时,ex≥a,f(x)=ex-ax+alna-a,
∵f′(x)=ex-a≥0,
∴f(x)在[lna,+∞)上为增函数,
当x≤lna时,ex≤a,f(x)=ax-ex-alna+a,
∵f′(x)=a-ex≥0,
∴f(x)在(-∞,lna]上为增函数,
综上所述,f(x)在定义域R内为增函数;
(2)易知F(x)的定义域为R,F′(x)=u′(x,a)-u′(x,b),而0<a<b,
∴lna<lnb,由(1)容易得到下列结论:
①当x≤lna<lnb时,F′(x)=(a-ex)-(b-ex)=a-b<0,
∴F(x)在(-∞,lna]上为减函数,从而F(x)≥F(lna),
②lna≤x≤lnb时,F′(x)=(ex-a)-(b-ex)=2ex-(a+b),
令F′(x)=0,得x=ln
| a+b |
| 2 |
当lna≤x<ln
| a+b |
| 2 |
当ln
| a+b |
| 2 |
∴当x=ln
| a+b |
| 2 |
| a+b |
| 2 |
③lna<lnb≤x时,F′(x)=(ex-a)-(ex-b)=b-a>0,
∴F(x)在[lnb,+∞)上为增函数,从而F(x)≥F(lnb)
综上所述,当x=ln
| a+b |
| 2 |
F(x)有最小值F(ln
| a+b |
| 2 |
| a+b |
| 2 |
(3)由(2)知T(a,b)=alna+blnb-(a+b)ln
| a+b |
| 2 |
要证T(a,b)>0,即证alna+blnb>(a+b)ln
| a+b |
| 2 |
等价为证:
| alna+blnb |
| 2 |
| a+b |
| 2 |
| a+b |
| 2 |
设g(x)=xlnx,则
上式等价为
| f(a)+f(b) |
| 2 |
| a+b |
| 2 |
即证明函数g(x)为凹函数即可.
∵g'(x)=1+lnx,g''(x)=
| 1 |
| x |
∴函数g(x)为凹函数,
即
| f(a)+f(b) |
| 2 |
| a+b |
| 2 |
∴alna+blnb>(a+b)ln
| a+b |
| 2 |
∴T(a,b)>0.
点评:本题主要考查导数的应用,利用函数单调性,极值和最值与导数之间的关系是解决本题的关键,考查构造函数思想与抽象思维与推理证明的能力,综合性较强,运算量较大,属于难题.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
阅读如图的程序框图,则输出的S=( )


| A、7 | B、8 | C、15 | D、24 |
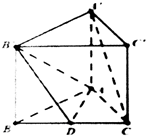 如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2
如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2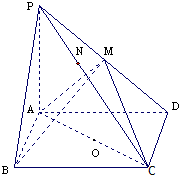 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.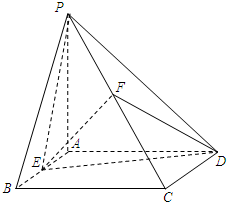 如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD.△PAD为等腰直角三角形,且PA⊥AD. E,F分别为底边AB和侧棱PC的中点.
如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD.△PAD为等腰直角三角形,且PA⊥AD. E,F分别为底边AB和侧棱PC的中点.