题目内容
已知tanα=2，求
．
| cos2α+sin4α |
| 1+cos2α+cos4a |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：由tanα的值，利用万能公式求出sin2α与cos2α的值，原式利用二倍角的正弦、余弦函数公式化简后，将各自的值代入计算即可求出值．
解答：
解：∵tanα=2，
∴sin2α=
=
=
，cos2α=
=
=-
，
则原式=
=
=
=-13．
∴sin2α=
| 2tanα |
| 1+tan2α |
| 4 |
| 1+4 |
| 4 |
| 5 |
| 1-tan2α |
| 1+tan2α |
| 1-4 |
| 1+4 |
| 3 |
| 5 |
则原式=
| cos2α+2sin2αcos2α |
| cos2α+2cos22α |
| 1+2sin2α |
| 1+2cos2α |
1+
| ||
1-
|
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
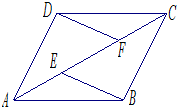如图，E、F是四边形ABCD的对角线AC上的两点，AE=CF，BE=DF，BE∥DF，AD=DC求证：四边形ABCD是菱形．
如图，是一个几何体的三视图，其中俯视图是正三角形，求：
用红黄蓝三种颜色给如图所示的六连圆涂色，若每种颜色只能涂两个圆，且相邻两个圆所涂颜色不能相同，则不同的涂色方案共有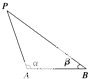
外国船只除特许外，不得进入离我国海岸线d海里以内的区域，如图所示，设A与B是我们的观测站，A与B的距离为s海里，海岸线是过A、B的直线，一外国船只在P点，在A站测得∠BAP=α，同时在B站测得∠ABP=β，则α与β满足三角不等式为