题目内容
直线l：xtan
+y+1=0的倾斜角α= ．
| π |
| 5 |
考点：直线的倾斜角
专题：直线与圆
分析：设直线的倾斜角为θ，易得直线的斜率，由斜率为倾斜角的关系可得tanθ=-tan
，结合倾斜角的范围，分析可得答案．
| π |
| 5 |
解答：
解：根据题意，设直线的倾斜角为θ，有0≤θ＜π，
直线可化为y=-tan
•x，
由倾斜角与斜率的关系，
可得tanθ=-tan
，
又有0≤θ＜π，
则θ=
，
故答案为：
．
直线可化为y=-tan
| π |
| 5 |
由倾斜角与斜率的关系，
可得tanθ=-tan
| π |
| 5 |
又有0≤θ＜π，
则θ=
| 4π |
| 5 |
故答案为：
| 4π |
| 5 |
点评：本题考查直线倾斜角的计算，注意倾斜角与斜率的关系即可．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
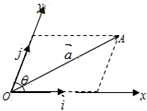已知单位向量