题目内容
已知三个平面向量
，
，
满足|
|=1，|
|=2，|
|=
，点E是BC的中点，若点D满足
=2
，则
•
= ．
| AB |
| AC |
| BC |
| AB |
| AC |
| BC |
| 3 |
| BD |
| AE |
| AC |
| AD |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：可得△ABC为直角三角形，且∠ABC为直角，建立平面直角坐标系，可求D的坐标，进而可得向量
和
的坐标，可得数量积．
| AC |
| AD |
解答：
解：∵|
|=1，|
|=2，|
|=
，
∴△ABC为直角三角形，且∠ABC为直角，
故可建立如图所示的平面直角坐标系，
可得A（0，1），B（0，0），C（
，0），
E（
，0），设D（x，y），
∴
=（x，y），
=（
，-1），
∵
=2
，∴
，即D（
，-2），
∴
=（
，-1），
=（
，-3），
∴
•
=
×
+（-1）×（-3）=6
故答案为：6．
解：∵|| AB |
| AC |
| BC |
| 3 |
∴△ABC为直角三角形，且∠ABC为直角，
故可建立如图所示的平面直角坐标系，
可得A（0，1），B（0，0），C（
| 3 |
E（
| ||
| 2 |
∴
| BD |
| AE |
| ||
| 2 |
∵
| BD |
| AE |
|
| 3 |
∴
| AC |
| 3 |
| AD |
| 3 |
∴
| AC |
| AD |
| 3 |
| 3 |
故答案为：6．
点评：本题考查平面向量数量积的运算，建立平面直角坐标系是解决问题的关键，属中档题．
练习册系列答案
相关题目
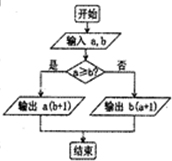如图，定义某种运算S=a?b，运算原理如图所示，则式子（2tan