题目内容
正方体ABCD-A1B1C1D1的8个顶点中任取4个连接构成的三棱锥中，满足任意一条棱都不与其表面垂直的三棱锥的个数（ ）| A、22 | B、24 | C、26 | D、28 |
考点：计数原理的应用
专题：应用题,排列组合
分析：分类讨论，在正方体一个面的四个顶点中任取三个点，在与这个面平行的面中只有一个顶点与刚才的三个顶点能构成符合条件的三棱锥；正四面体A1C1BD和正四面体ACB1D1也符合条件，即可得出结论．
解答：
解：不妨在正方体一个面的四个顶点中任取三个点，在与这个面平行的面中只有一个顶点与刚才的三个顶点能构成符合条件的三棱锥（如图中三棱锥D1-ABC），所以这一对平行平面的顶点共构成2×
=8个符合条件的三棱锥，正方体中共有三对平行平面，所以可构成符合条件的三棱锥3×8=24个．
另外正四面体A1C1BD和正四面体ACB1D1也符合条件，
故符合条件的三棱锥共有24+2=26个．
故选：C
| C | 3 4 |
另外正四面体A1C1BD和正四面体ACB1D1也符合条件，
故符合条件的三棱锥共有24+2=26个．
故选：C
点评：本题考查排列组合知识，正确分类是关键．
练习册系列答案
相关题目
抛物线C1：y=ax2（a＞0）的焦点与双曲线C2：
-y2=1的右焦点的连线交C1于第一象限的点M，若C1在点M处的切线平行于C2的一条渐近线，则a=（ ）
| x2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知复数z=（x2-1）+（x+1）i（x∈R，i是虚数单位）是纯虚数，则x的值为（ ）
| A、-1 | B、1 | C、±1 | D、0 |
已知f（x）=cos2（x-
），若f（α）=p，则f（-α）=q，则下列等式一定成立的是（ ）
| π |
| 4 |
| A、p-q=0 |
| B、p+q=0 |
| C、p+q-1=0 |
| D、p-q+1=0 |
在△ABC中，内角A，B，C的对边分别为a，b，c，若sin2B-sin2C=
sinCsinA，a=2
c，则B=（ ）
| 3 |
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
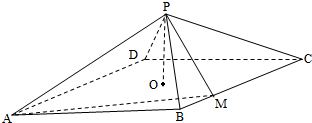如图，四棱锥P-ABCD，底面是以O为中心的菱形，PO⊥底面ABCD，AB=2，∠BAD=